什么是堆
堆是一种特殊的二叉树,具备以下特性:
- 堆是一个完全二叉树(不一定是二叉排序树)
- 每个节点的值都必须大于等于(或小于等于)其左右孩子节点的值
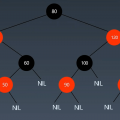
如果每个节点的值都大于等于左右孩子节点的值,这样的堆叫大顶堆;如果每个节点的值都小于等于左右孩子节点的值,这样的堆叫小顶堆:
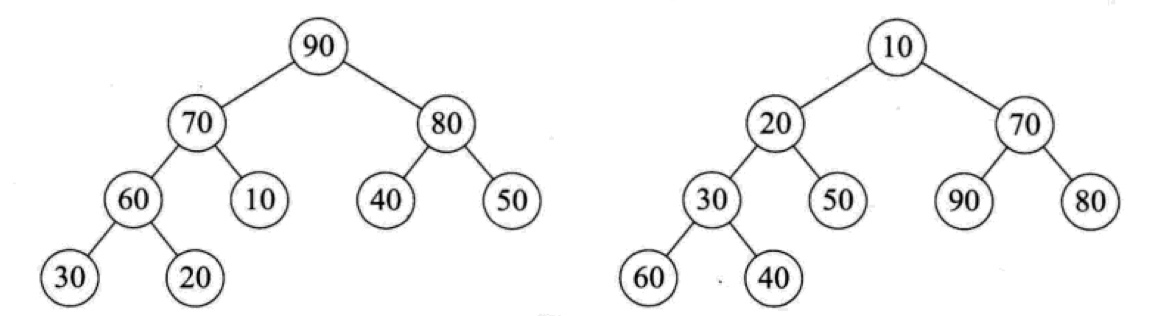
上图中,左侧的堆是大顶堆,右侧的堆是小顶堆,我们还可以得出这个结论:对应大顶堆,堆顶一定是最大值;对于小顶堆,堆顶一定是最小值。
如何构建堆
我们在介绍二叉树的定义和存储的时候说到,由于完全二叉树的特殊性,可以通过数组来存储,堆也是完全二叉树,所以我们完全可以通过数组来存储。在使用数组存储堆的时候,把第一个索引位置留空,从第二个索引位置开始存储堆元素,这样,对于索引值为 i 的元素而言,其子节点索引分别为 2i 和 2i+1。
下面我们就来看如何在堆中插入新节点,以大顶堆为例,从叶子结点插入,如果比父级元素大,则与父级元素交换位置,依次类推,直到到达根节点(小顶堆恰好相反):
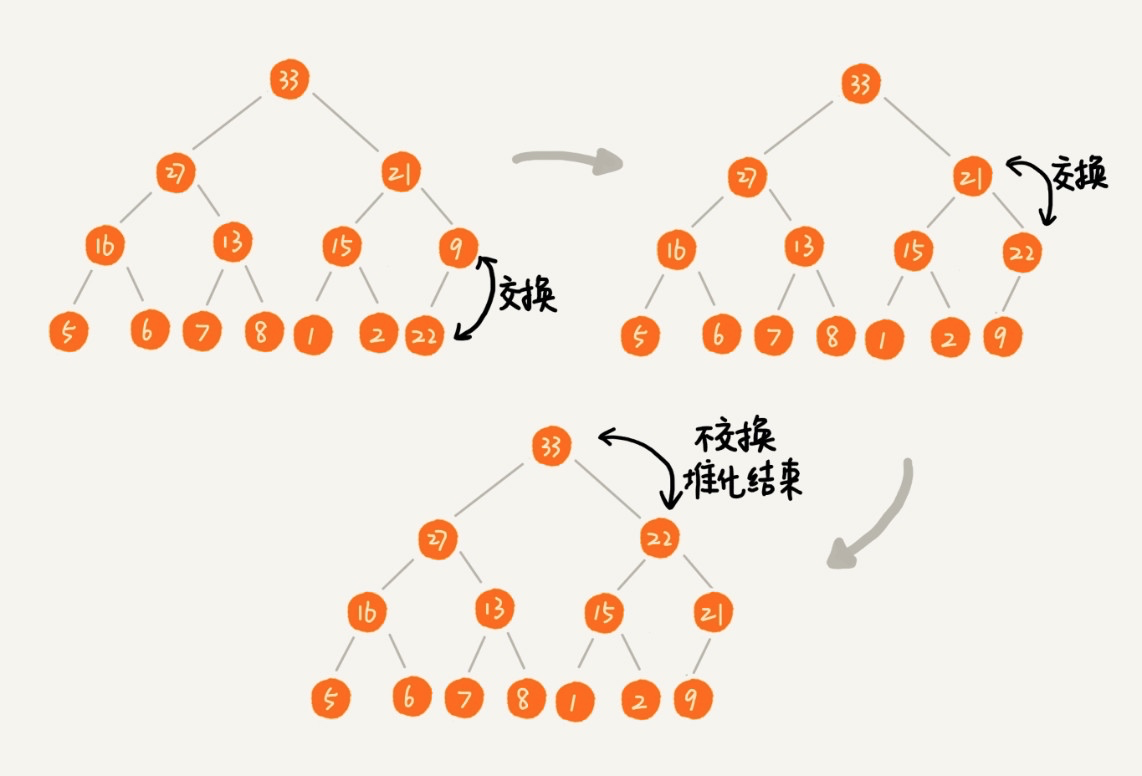
构建堆的过程叫堆化。
实现代码
下面是对应的 Go 堆化实现代码(仅包含插入节点):
package heap
// Heap 通过数组切片存储二叉树节点
type Heap []int
func New() *Heap {
return new(Heap)
}
func (h *Heap) Len() int {
return len(*h)
}
// Less 比较元素大小
func (h *Heap) Less(i, j int) bool {
return (*h)[i] < (*h)[j]
}
// Swap 交换元素位置
func (h *Heap) Swap(i, j int) {
(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}
// Push 新增节点
func (h *Heap) Push(v interface{}) {
*h = append(*h, v.(int))
i := h.Len() - 1 // 新增元素位置
for {
j := (i - 1) / 2 // 父节点位置
// 如果是根节点或者父节点值大于子节点值,则退出循环
if i == j || !h.Less(i, j) {
break
}
// 否则交换子节点与父节点,直到父节点值大于子节点
h.Swap(i, j)
i = j
}
}
可以看到,上面构建的是一个小顶堆,为了简化演示,我们通过一个整型切片存储底层的二叉树结构。接下来我们可以为这段代码编写测试用例:
package heap_test
import (
"testing"
"github.com/geekr-dev/go-algorithms/tree/heap"
)
func verify(t *testing.T, h *heap.Heap, i int) {
t.Helper()
n := h.Len()
j1 := 2*i + 1 // 左子节点
j2 := 2*i + 2 // 右子节点
if j1 < n {
if h.Less(j1, i) { // 左子节点小于父节点值
t.Errorf("堆特性已破坏: [%d] = %d > [%d] = %d", i, h[i], j1, h[j1])
return
}
verify(t, h, j1)
}
if j2 < n {
if h.Less(j2, i) { // 右子节点小于父节点值
t.Errorf("堆特性已破坏: [%d] = %d > [%d] = %d", i, h[i], j1, h[j2])
return
}
verify(t, h, j2)
}
}
func TestHeapPush(t *testing.T) {
h := heap.New()
for i := 10; i > 0; i-- {
h.Push(i)
}
verify(t, h, 0)
}
测试代码运行通过,则表示堆化成功:

堆排序
前面我们介绍了堆的定义及构建,接下来我们来分享堆排序及应用,堆排序的过程其实就是不断删除堆顶元素的过程。如果构建的是大顶堆,逐一删除后堆顶元素构成的序列是从大到小排序;如果构建的是小顶堆,逐一删除堆顶元素后构成的序列是从小到大排序。而这其中的原理,就是我们在前面提到的:对于大顶堆,堆顶一定是最大值;对于小顶堆,堆顶一定是最小值。
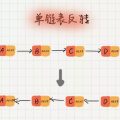
但是这里有一个问题,每次从堆顶删除元素后,需要从子节点中取值补齐堆顶,依次类推,直到叶子节点,就会致使存储堆的数组出现「空洞」:
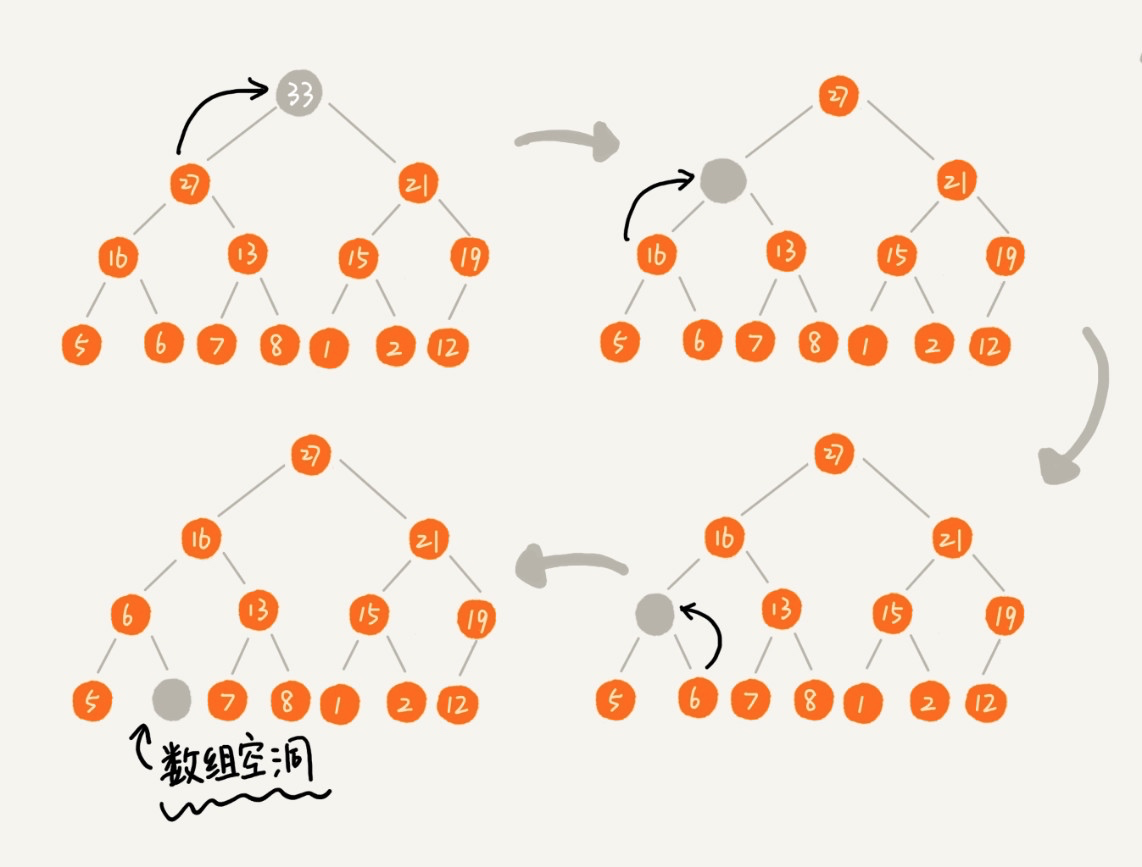
解决办法是将数组中的最后一个元素(最右边的叶子节点)移到堆顶,再重新对其进行堆化:
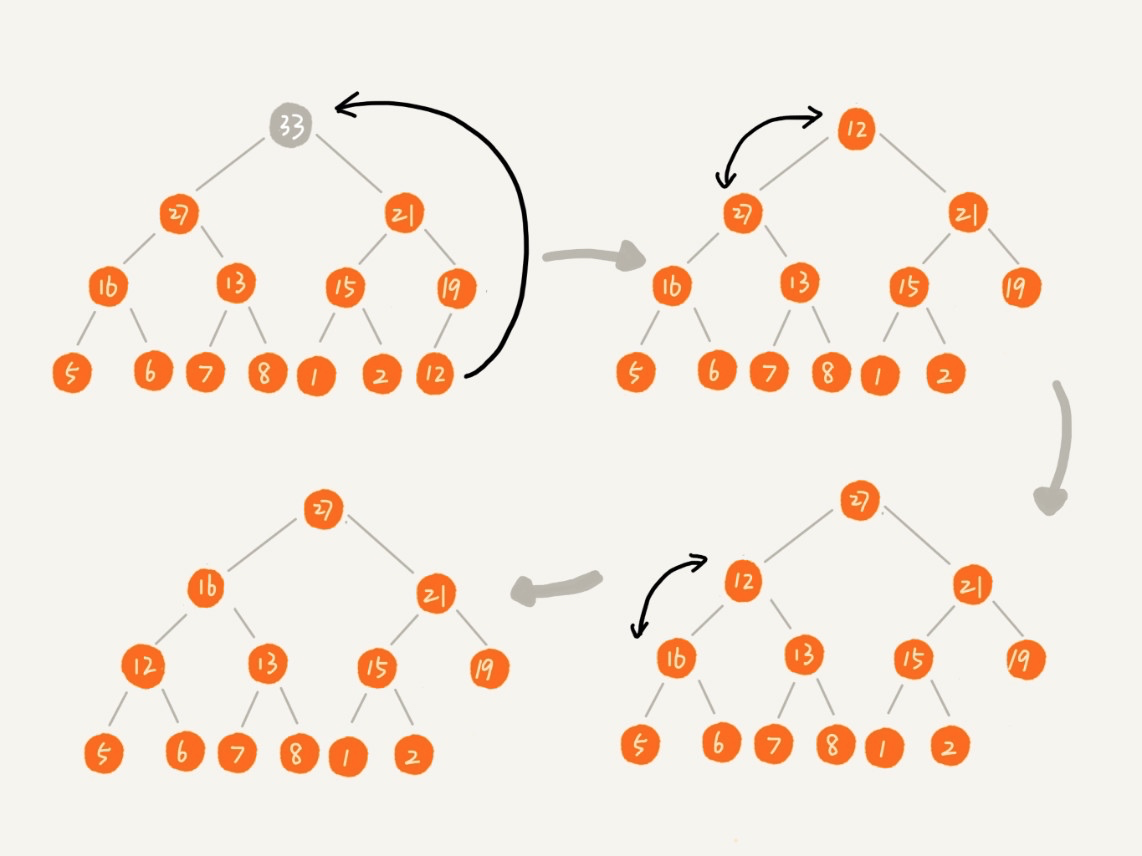
这样,就完美解决了「数组空洞」的问题。
实现代码
下面我们将堆排序过程转化为对应的 Go 实现代码如下,其实就是补上删除节点的方法:
// Pop 弹出堆顶元素并删除
func (h *Heap) Pop() (v interface{}) {
// 将堆顶元素和最后一个元素交换位置,解决数组空洞问题
n := h.Len() - 1
h.Swap(0, n)
// 剩余元素重新堆化
i := 0
for {
j1 := 2*i + 1 // 左子节点
if j1 >= n || j1 < 0 { // 数组越界,则退出
break
}
j := j1
// 如果i对应节点的右子节点比左子节点值小
if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
j = j2 // = 2*i + 2 // 右子节点
}
// 左/右子节点值已经大于父节点值,则退出
if !h.Less(j, i) {
break
}
// 否则交换左/右子节点较小值对应节点与父节点的位置,继续循环,知道堆化成功
h.Swap(i, j)
i = j
}
*h, v = (*h)[:h.Len()-1], (*h)[h.Len()-1] // 注意此时最后一个节点(待删除节点)已经从切片中剔除,随时会被gc
return v
}
我们可以结合堆化和删除方法,写一段测试代码:
func TestHeapPop(t *testing.T) {
h := heap.New()
// 先插入
for i := 10; i > 0; i-- {
h.Push(i)
}
// 再弹出
for h.Len() > 0 {
n := h.Pop()
fmt.Printf("%d ", n)
verify(t, h, 0)
}
fmt.Println()
}
运行这个测试方法:

打印结果如上,说明堆排序成功,数据变成了从小到大的排序序列。
复杂度分析
我们先看时间复杂度,对堆排序而言,分为两个阶段,一个是堆的构建,一个是堆顶元素的删除。对于 n 个节点的堆化而言,通过数组存储,对应的时间复杂度是 O(n),对于堆顶元素的删除而言,需要遍历 n 个节点,并且,每次删除后需要重新堆化,对应的平均时间复杂度是 O(nlogn)。所以综合下来,堆排序的时间复杂度和快速排序、归并排序一样,是 O(nlogn)。
堆排序的过程中,涉及到不相邻元素的交换(删除堆顶元素的时候),所以不是稳定的排序算法。