介绍完基本的线性表排序算法后,今天我们来介绍一种常见的线性表查找算法 —— 二分查找。
二分查找的引入
对于基于数字索引的数组/切片元素查找,我们可能第一反应都是遍历这个数组/切片,直到给定元素值和待查找的值相等时,返回索引值并退出,否则一直遍历到最后一个元素,如果还是没有找到则返回 -1。
这样的查找虽然是简单粗暴了点,但是对于规模不大的数据集,也是没什么问题的,不过很明显,对于 n 个元素的数组,这种查找的时间复杂度是 O(n),随着数据规模的增加,性能会越来越差,设想如果数据集的长度是 40 亿(约为 2 的 32 次方),那么最差的情况下需要遍历数组 40 亿次,简直不敢想象需要花费多长时间!那有没有性能更好的算法来解决这个问题呢?
在进一步探讨这个问题之前,我们先来看一个生活中的例子。我们日常生活中,很多人应该有这种经历,朋友、同学或者同事淘了个宝贝,神秘兮兮的过来让大家猜多少钱,在约定一个价格范围之后(比如 10-100),大家会七嘴八舌的猜起价格来:
同事 A:新淘了个宝贝,猜猜多少钱?
同事 B:50块。
同事 A:高了!
同事 C:30块。
同事 A:低了!
同事 D:40块。
同事 A:高了!
同事 E:36块。
同事 A:对了!
如果我们用顺序遍历的逻辑,最差需要 91 次,才能猜到价格,现实生活中,没人会这么干,我们采用上面这种逻辑,只需要 4 次就猜到价格了,快了几十倍,而且数据量越大,优势越明显。基于这种思路,我们的算法科学家提炼出了二分查找算法,帮助我们在给定数据集中快速定位要查找的元素。
实现原理
所谓二分查找,针对的是一个有序的数据集合(这点很重要),查找思想有点类似分治思想 —— 每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。图示如下:
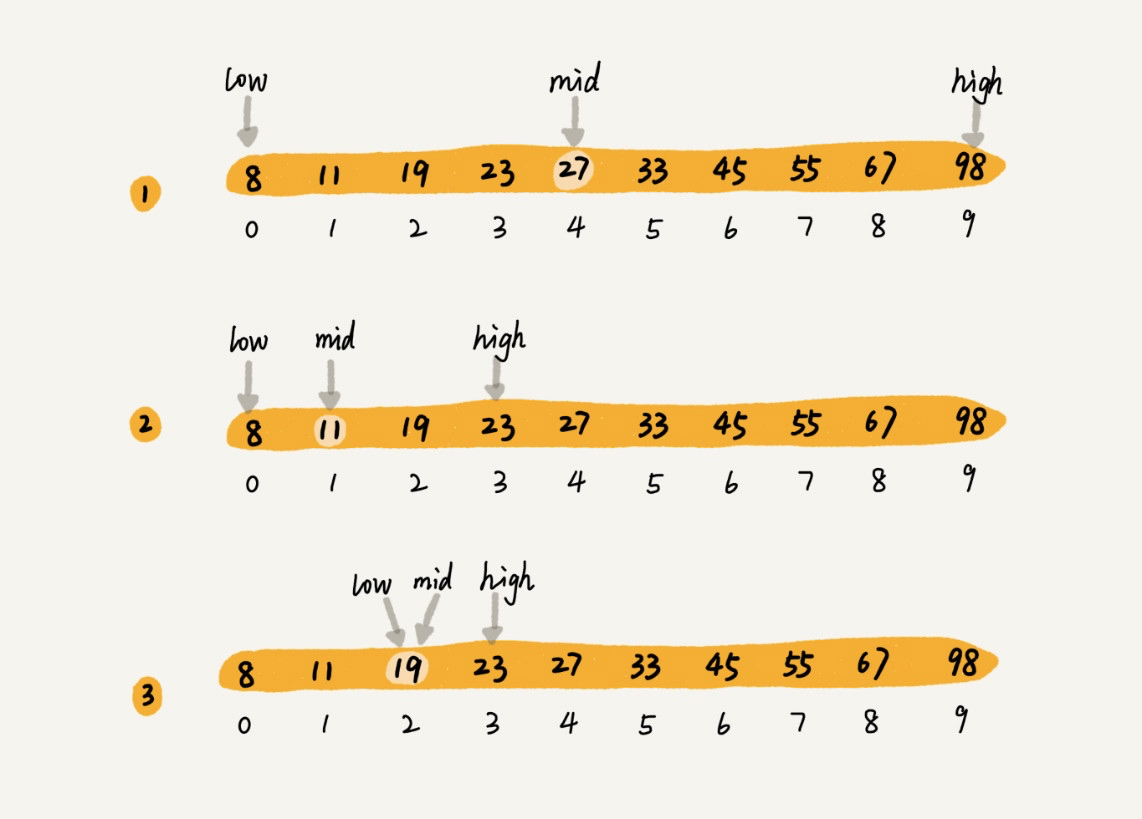
注意:二分查找针对的必须是已经排序过的有序数据序列,否则不能使用该算法。
示例代码
二分查找的思路比较简单,我们通过 Go 代码实现如下:
package main
import (
"fmt"
"sort"
)
// 二分查找实现代码
func binarySearch(nums []int, num int, low int, high int) int {
// 递归终止条件
if low > high {
return -1
}
// 通过中间元素进行二分查找
mid := (low + high) / 2
// 递归查找
if num > nums[mid] {
// 如果待查找数据大于中间元素,则在右区间查找
return binarySearch(nums, num, mid + 1, high)
} else if num < nums[mid] {
// 如果待查找数据小于中间元素,则在左区间查找
return binarySearch(nums, num, low, mid - 1)
} else {
// 找到了,返回索引值
return mid
}
}
func main() {
nums := []int{4, 6, 5, 3, 1, 8, 2, 7}
sort.Ints(nums) // 先对待排序数据序列进行排序
fmt.Printf("Sorted nums: %v\n", nums)
num := 5
index := binarySearch(nums, num, 0, len(nums)-1)
if index != -1 {
fmt.Printf("Find num %d at index %d\n", num, index)
} else {
fmt.Printf("Num %d not exists in nums\n", num)
}
}
对于未排序的数据序列,需要先排序,才能使用二分查找算法,这里我们使用了 Go 内置的 sort.Ints 对整型切片进行排序,你也可以使用前面介绍的排序算法实现同样的排序效果。
执行上述代码,打印结果如下:

性能分析
很显然,二分查找的时间复杂度是 O(logn)。这是一个非常恐怖的数量级,有时候甚至比 O(1) 还要高效,比如我们要在开头提到的 40 亿个数字中查找某一个元素,也只需要32次(2 的 32 次方是 40 亿数量级),这真的是非常高效了,正因如此,二分查找在线性表结构中的应用非常广泛。
但是使用二分查找需要注意一个前提,那就是针对有序数据序列,换言之,二分查找适用于变动不是很频繁的静态序列集,如果序列集变动很频繁,经常进行插入删除操作,那么就要不断维护这个序列集的排序,这个成本也很高,因此,这种情况下就不适用二分查找了,比如我们的数据库查询,增删改查很频繁,显然不是通过二分查找来进行查询的。
对于这种动态数据集,要同时保证更新(包含插入和删除)和查询的高效,通常有两种方案,一种是哈希表,一种是树结构,比如 Redis 底层就是基于哈希表的,而 MySQL 底层则是基于 B+ 树。关于哈希表和树结构,我们后面会详细介绍。