树的相关概念
树这种数据结构模拟了自然界中树的概念,自然界中的树有根、叶子、枝干,数据结构中的树也是如此,只不过是倒过来的:
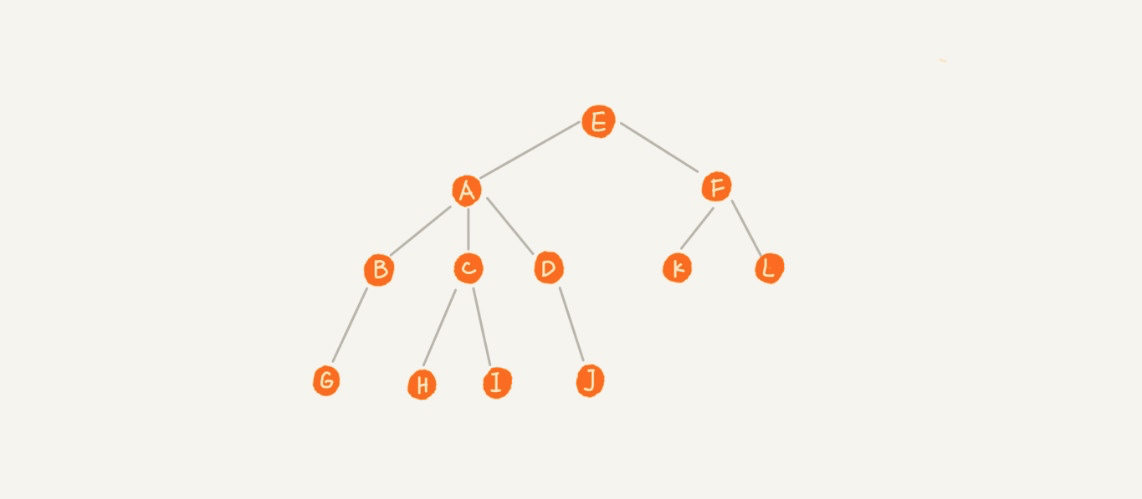
其中的每个元素叫做节点。树的顶点(没有父元素的节点)叫根节点,如 E;每个分支的末端节点(没有子元素的节点)叫叶子节点,如 G、H、I、J、K、L;用来连接相邻节点之间的关系叫父子关系,比如 E 是 A、F 的父节点,A、F 是 E 的子节点;具有同一个父节点的多个子节点叫做兄弟节点,比如 A、F 是兄弟节点。
节点拥有的子节点数目叫做节点的度,显然,叶子节点的度为 0,树的度是树内各节点度的最大值。
除此之外,树还有高度、深度和层的概念:

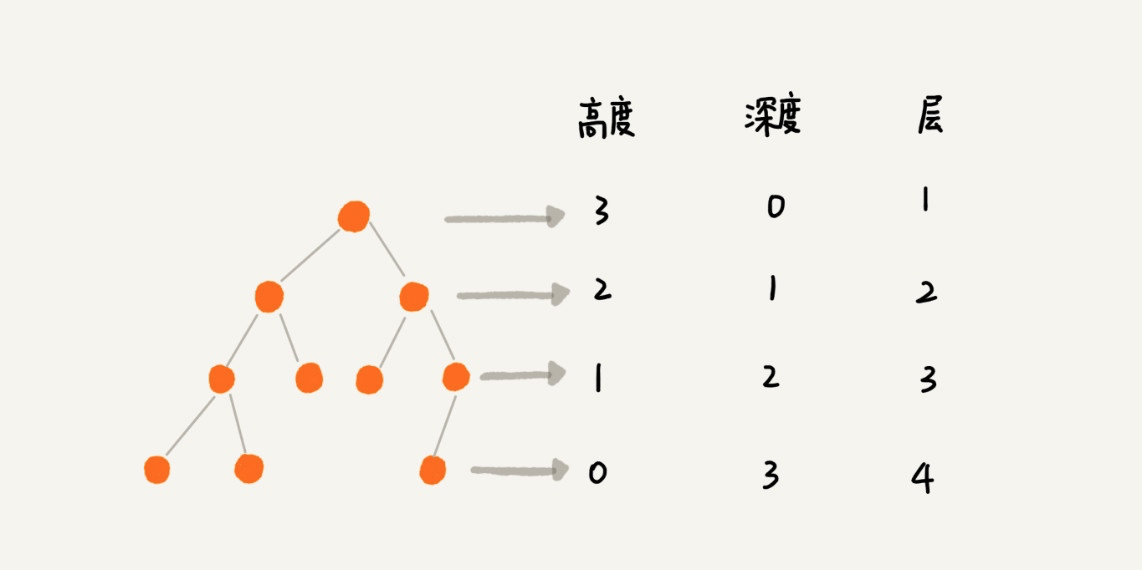
注:其实线性表也可以看作一种特殊的树,只不过所有节点都在一个分支上,第一个元素是根节点,最后一个元素是子节点,没有兄弟节点。层数就是线性表的长度。
多个互不相交的树可以构成森林。
二叉树的定义
二叉树是我们平时遇到的最常见的树结构,它是一种特殊的树,顾名思义,就是每个节点最多有两个「分叉」,即两个子节点,分别是左子节点和右子节点,不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子结点,有的节点只有右子节点。比如下面这些都是二叉树:
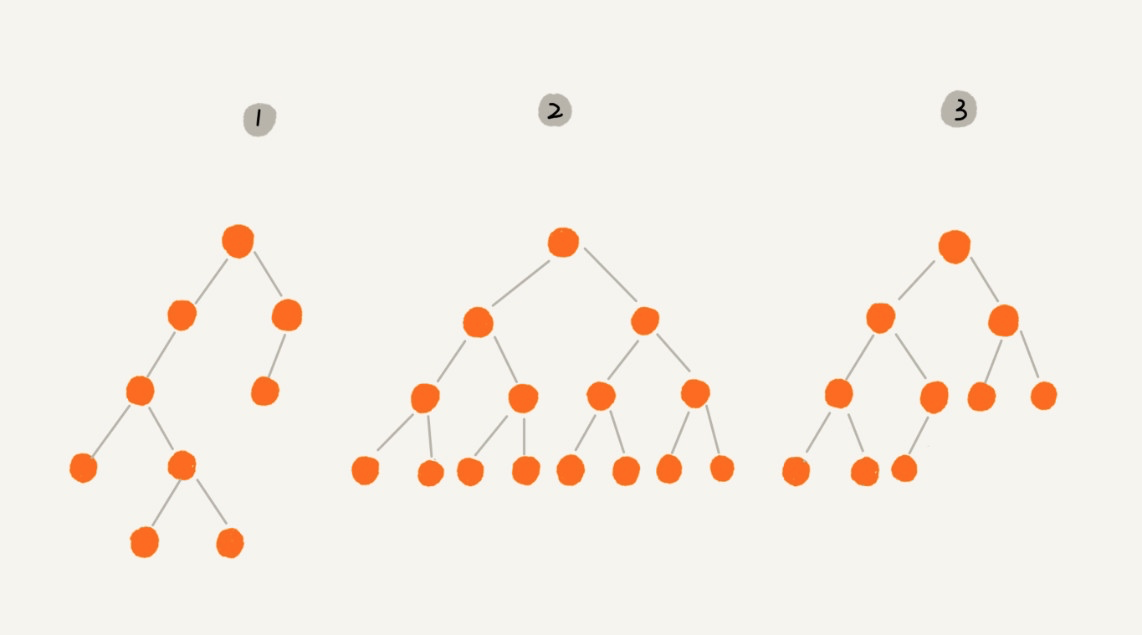
根据左右子节点的饱和度,我们又从二叉树中提取出两种特殊的二叉树 —— 满二叉树和完全二叉树。满二叉树即所有分支节点都有左右子节点,并且所有叶子节点都在同一层上,如上面的图2便是满二叉树。完全二叉树要复杂一些,深度为 k 有 n 个节点的二叉树,当且仅当其中的每一节点,都可以和同样深度 k 的满二叉树,序号为 1 到 n 的节点一对一对应时,称为完全二叉树,比如上面的图3就是完全二叉树。
二叉树的特性
在讨论二叉树的创建和存储之前,我们先来总结下二叉树的一些特性,以便后续用到(这里二叉树数的深度定义采用的最大层次数,如果从 0 开始计算的话,可以自行推演一下):
性质1:
在第 i 层最多有 2i-1 个节点。
性质2:
深度为 k 的二叉树最多有 2k-1 个节点。
性质3:
对于任何一个二叉树,叶子节点数为 n0,度为 2 的节点数为 n2,则 n0 = n2+1。
性质4:
性质5:

树这种结构不能简单通过线性表的前后关系来存储,在线性表中,一个节点只有至多一个前驱节点和至多一个后驱节点,树则不然,一个节点可能有多个后驱节点,这个时候,我们需要通过更加复杂的结构才能存储树。
二叉树是一种特殊的树,比多叉树要简单,因为特定节点至多只有两个节点,这就极大简化了相应的数据结构,使得通过线性表就可以实现二叉树的存储。我们后面基本只讨论二叉树,下面我们通过数组和链表来演示如何存储二叉树。
通过数组存储二叉树
对于特定的二叉树而言,比如满二叉树、完全二叉树,它们的节点之间是有一定关联关系的,以下面这棵完全二叉树为例:
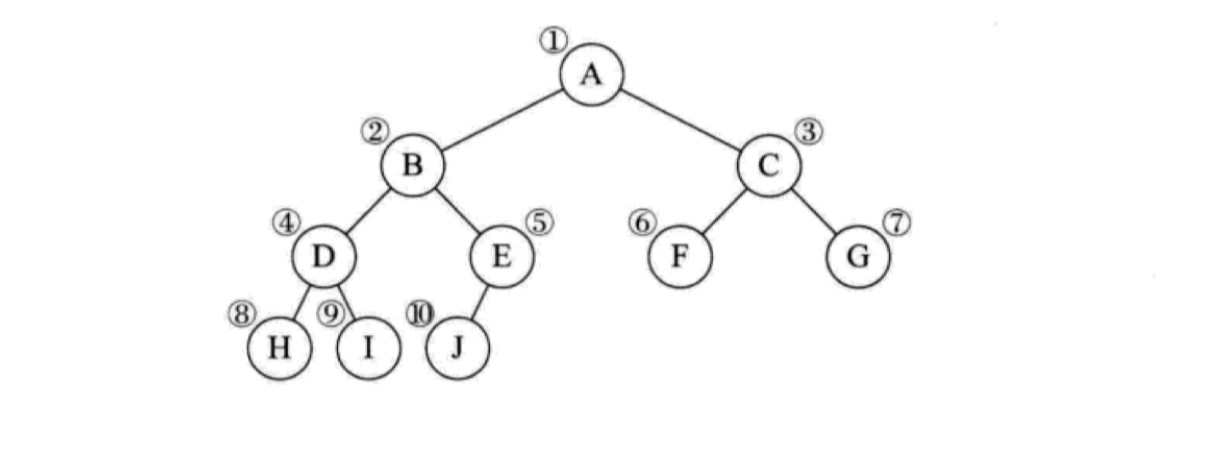
我们按照从上到下,从左到右对所有节点编号,可以看到,下一层的左右子节点和对应父节点序号存在某种数学关系,如果父节点的序号是 i,其对应左子节点位于 2i 的位置上,对应右子节点位于 2i + 1 的位置上,我们可以参照这个规则将上述完全二叉树存储到数组中:
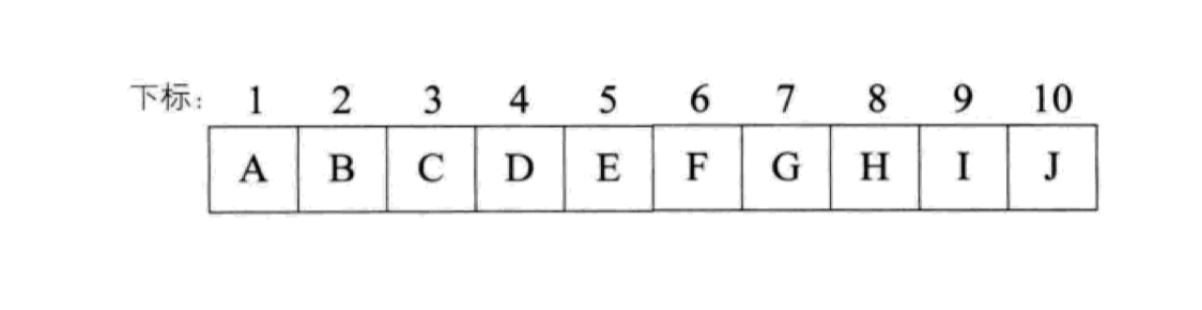
注意我们的下标从 1 开始(根节点),索引为 0 的下标舍弃,浪费这个空间,以方便计算。这样,我们就可以从根节点开始,依次将所有节点元素存放到数组中,并且可以根据节点间的数学关系很方便地遍历整棵树。此外,由于完全二叉树的特殊性,除了第一个元素之外,该数组不存在任何空间的浪费。由于满二叉树是完全二叉树的子集,所以也可以通过这种方式来存储。
那么其它二叉树呢?当然也可以按照这种思路来做,我们把不存在的节点补全,比如假设上述序号为 4、6、8、9 的元素不存在:
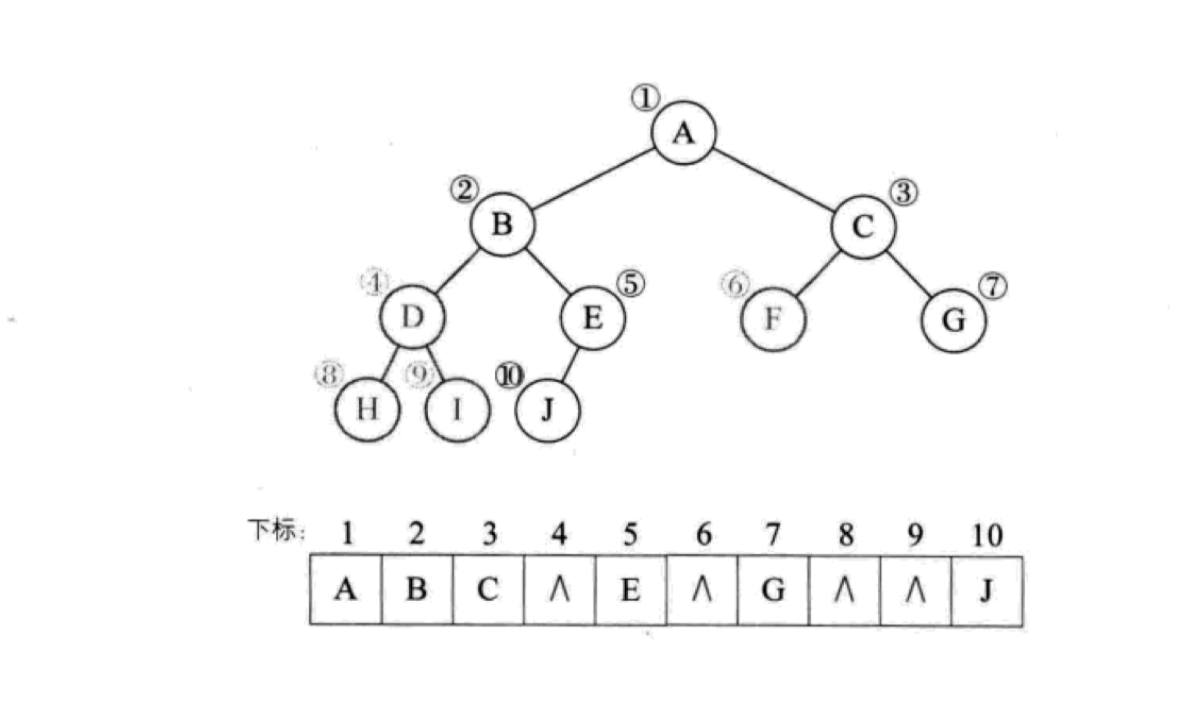
可以看到,我们将不存在的元素补上,只是对应位置值为 null,缺失的节点越多,数组的「空洞」也就越多,如果是极端情况,比如二叉树只包含 1、3、7 三个元素,那么数组中将会存在大量的「空洞」,浪费大量的空间,而且也会影响性能。
综上,数组适合满二叉树、完全二叉树这些特殊二叉树的存储,一些比较稠密的二叉树也可以用数组,如果二叉树比较稀疏就不适合用数组了,我们可以通过链表来存储它们。
通过链表存储二叉树
理论上来说,链表适用于所有的二叉树存储,只不过这里我们需要对线性表中的链表进行扩展,因为二叉树特定节点最多有两个子节点,所有我们在链表结点上设置两个指针域,分别指向左右子节点,所以这种链表结构又被称作二叉链表。我们可以通过一个结构体表示二叉链表的节点:
// 节点类
type Node struct {
Value string
Left *Node
Right *Node
}
// 初始化根节点
func NewNode(data string) *Node {
return &Node{data, nil, nil}
}
如果要用二叉链表表示上面的完全二叉树,对应的图示如下:
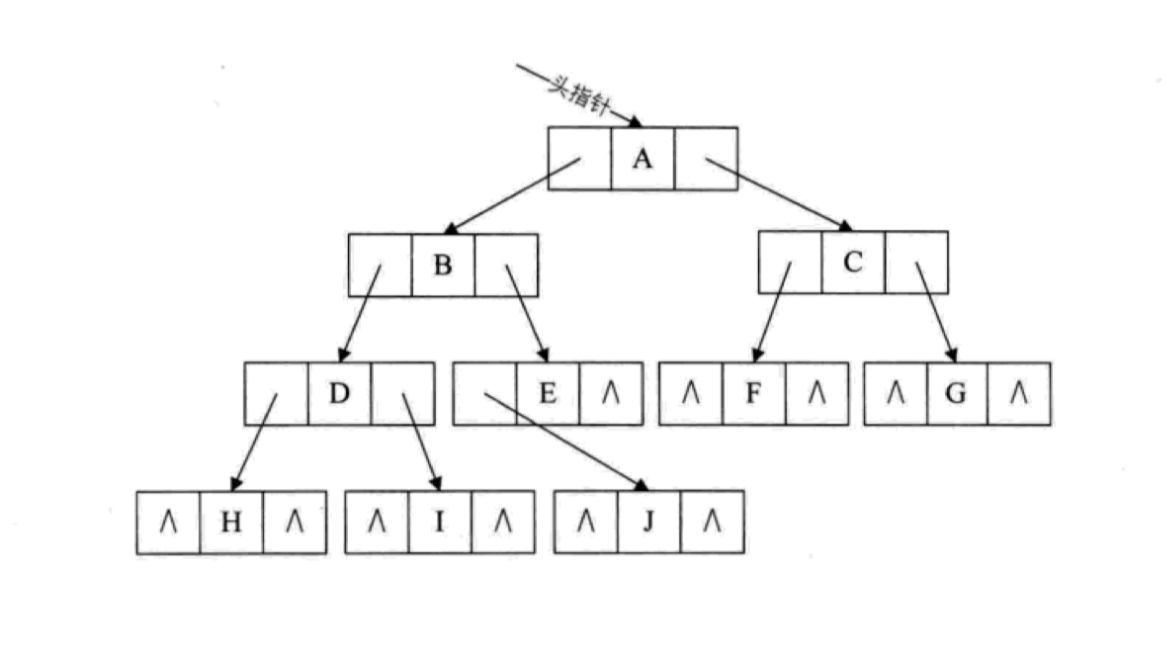
不管是什么样结构的二叉树,用链表来存储都不会存在空间的浪费。关于二叉树的创建、查找和删除,需要等到介绍完二叉树的遍历才能开始,下一篇我们就来探讨如何遍历二叉树。