在上篇教程中,学院君给大家介绍了平衡二叉树的定义、实现原理、构建过程演示以及对应的实现代码,我们提到平衡二叉树是最理想的二叉排序树,性能最好,也最稳定,但是缺点是维护成本高,需要在插入和删除节点时维护新树的平衡性,所以在工程实践中,我们倾向于使用另一种二叉排序树 —— 红黑树。
什么是红黑树?红黑树的性能如何?如何实现红黑树?带着这些问题,我们开始今天的教程。
什么是红黑树
红黑树(Red-Black Tree)是一种每个节点都带有颜色属性的、近似平衡的二叉排序树,从 2-3 树衍生而来。所以在正式介绍红黑树之前,我们先来看看 2-3 树的构造。
从2-3 树开始
为了解决二叉排序树的不平衡,2-3 树孕育而生,2-3 树的节点不再是单一的 2 节点,节点可能是 2 节点、3 节点:
- 2 节点:存储一个值,最多有左右两个子树
- 3 节点:存储两个值,最多有左中右三个子树,如下图所示的方形框就是一个 3 节点

2-3 树的查找和二叉排序树的查找思路是相同的,不过不同的是在判断节点数值是否相同时 2-3 树要判断是否等于左值或右值,如果大于左值小于右值,需要从中子节点开始递归。
2-3 树的插入
2-3 树的插入有以下几种情况:
1)树为空
插入前树为空,则插入的节点作为根节点并且树变为 2 节点:

2)2节点插入
若插入的节点为 2 节点,则 2 节点会转化为 3 节点:

3)3 节点插入
若插入的节点为 3 节点,则临时调整 3 节点为 4 节点(三个值),接下来,又要做细分处理,当插入前父节点为空时,4 节点会转化为 3 个 2 节点,4 节点中的中值会变为左右值的父节点:

若插入前父节点为 2 节点,则 4 节点的中子转化为父节点的值,原来的父节点转化为 3 节点:

若插入前父节点为 3 节点,则 3 节点的中子节点转为父节点的值,父节点临时转化为 4 节点,此时就变成了插入的节点为 3 节点的情况上面的两种情况:


可以看到,2-3 插入节点后,最终是会自平衡的。
从2-3树到红黑树
接下来,我们再回到红黑树,红黑树其实是 2-3 树的一种只含 2 节点的表现形式。

如何表示3-节点呢?我们尝试一种特殊的边:默认情况下节点的颜色均为黑色,将某个节点染为红色,表示它和父亲的的链接是红色的,就像下图:

当我们将红链接画平时:

可以看到它和 2-3 树中的 3 节点极为相似。事实上,我们完全可以用这样的方式来表示 2-3 树中的 3 节点,下图是如何从 2-3 树演化成一棵典型红黑树的示例图:

具体的实现很简单:对于2节点,保持不变;对于3节点,我们首先将3节点中左侧的元素标记为红色;然后将3节点分拆成2节点(图3),再将3节点位于中间的子节点(4)的父节点设置为父节点中那个红色节点(3)的子节点(图4),最后将整棵树展开为图5所示的二叉树,就成了大名鼎鼎的红黑树了。
红黑树的特性
一棵标准的红黑树如下所示:
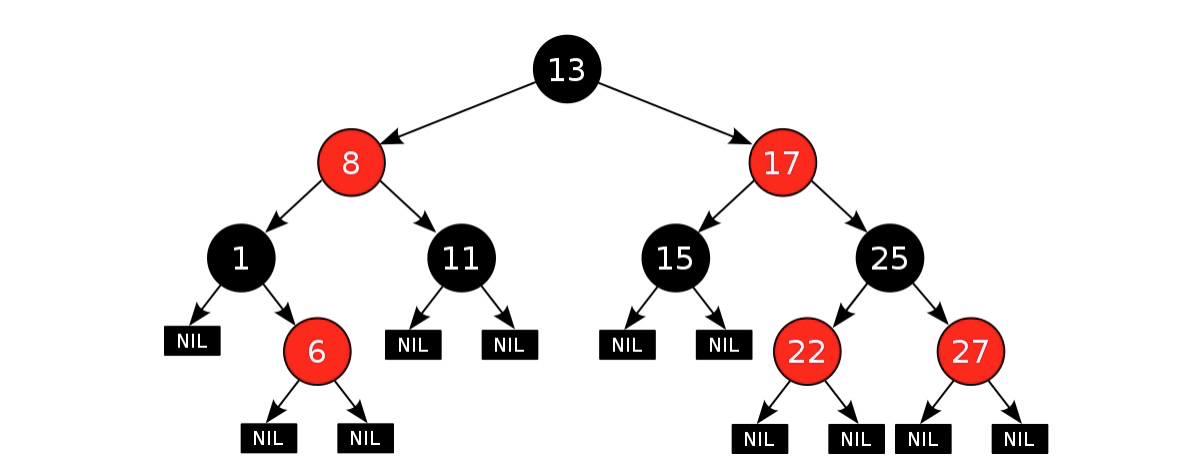
它必须具备以下特性:
- 节点是红色或黑色;
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点。
这些约束保证了红黑树的关键特性:从根节点到叶子节点的最长的可能路径不多于最短的可能路径长度的两倍(每条路径红黑相间,且黑色节点数目相同,所以最短的路径上是两个黑色节点,相应的,此时最长路径节点一定是黑-红-黑-红,正好是其两倍),从而保证红黑树无论怎么插入、删除节点,大致上也是平衡的。
红黑树的性能
我们上面提到由于红黑树的特性,可以确保即使在最差情况下,红黑树也是大致平衡的,下面我们来简单推导下红黑树的时间复杂度。
前面我们讲二叉排序树的时候说到二叉排序树的时间复杂度和树的高度成正比,红黑树是红黑相间的,我们可以先把红色的节点去掉,剩下的黑色节点就可能变成四叉树了,比如我们上面示例的那个红黑树。由于红黑树每条路径上黑色节点相同,所以可以继续把这个四叉树转化为完全二叉树,假设黑色节点的数量为 m,这样,这棵树的时间复杂度就是 O(logm) 了;然后我们把红色节点塞回来,红色节点的总数目肯定是小于等于黑色节点的,我们不妨假设等于黑色节点,这样,树的高度就增加一倍,对应的时间复杂度就是 2O(logm) 了,m≈n/2,由于在计算时间复杂度的时候,常量可以舍弃,所以红黑树的时间复杂度也是 O(logn)。虽然这里面都是估算的,但是由于前面提到的红黑树的特性约束,数量级上是没问题的。
红黑树维护成本比平衡二叉树低,性能上也能大致做到 O(logn),且比较稳定,可以应付最差的情况,所以工程上我们通常使用红黑树实现自平衡的二叉排序(查找)树,比如 Java 的 HashMap,MySQL 的 InnoDB 引擎底层都是通过红黑树实现数据存储的。
下篇教程,学院君会给大家演示红黑树的节点插入、删除和代码实现。