引子
上篇教程学院君给大家介绍了二叉排序树,并且提到理想情况下,二叉排序树的插入、删除、查找时间复杂度都是 O(logn),非常高效,而且它是一种动态的数据结构,插入删除性能和查找一样好,不像之前提到的二分查找,虽然查找性能也是 O(logn),但是需要先对线性表进行排序,而排序的最好时间复杂度也是 O(nlogn),所以二分查找不适合动态结构的排序。
但是我们也提到如果二叉排序树构造的不好的话就会退化成斜树:
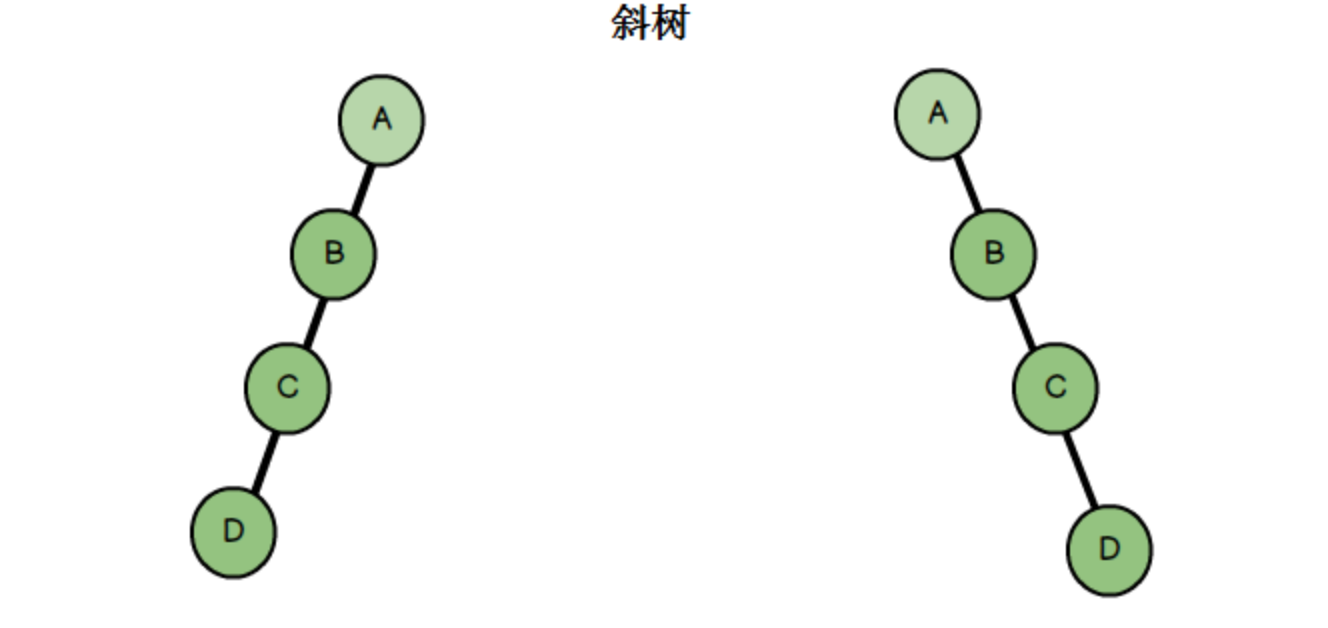
此时按照之前的实现算法性能退化成了 O(n),所以如何构造二叉排序树很重要,我们的理想情况是满二叉树和完全二叉树,它们的性能都是 O(logn),所以我们在构造二叉排序树的时候要尽可能向它们靠近,才能得到最佳的操作性能,由此引出了我们今天的话题 —— 平衡二叉树。
什么是平衡二叉树
平衡二叉树的英文名是 Self-Balancing Binary Search Tree 或者 Height-Balancing Binary Search Tree,译作自平衡的二叉搜索树,或者高度平衡的二叉搜索树,二叉搜索树和二叉排序树是一个意思,只是叫法不同,简称平衡二叉树,也叫 AVL 树(平衡二叉树作者的名字首字母)。
所以平衡二叉树首先是二叉排序树,并且这个二叉排序树是左右高度平衡的,这么讲有点抽象,具体来说,平衡二叉树要求每个节点的左子树和右子树的高度差至多等于 1,这个高度差的值叫做平衡因子 BF,也就是说 BF 的值不能大于1,否则就不是平衡二叉树。
我们简单看几个例子:

- 图1不满足平衡二叉树的定义,对 58 这个节点来说,平衡因子 BF 的值是 2,所以只是普通的二叉排序树;
- 图2所示二叉树不是二叉排序树,所有不是平衡二叉树;
- 图3不满足平衡因子小于等于1的要求,对 58 这个节点来说,平衡因子 BF 的值是 3,因而不是平衡二叉树;
- 图4满足平衡二叉树的定义,是平衡二叉树;
我们之所以这么约束平衡二叉树,是为了保证它能够始终做到插入、删除、查找的时间复杂度是 O(logn)。
了解了什么是平衡二叉树,下面我们来看看它的实现原理。
平衡二叉树的实现原理
平衡二叉树的基本实现思路,是在构建二叉排序树的时候,每插入一个节点,都要检查这个节点的插入是否破坏了原有的平衡性,如果是的话,则找出最小不平衡子树,在保证整体二叉排序树的前提下,通过左旋或者右旋的方式将其调整为平衡子树。从而动态维护这棵平衡二叉树。
这里面有几个概念需要解释一下:
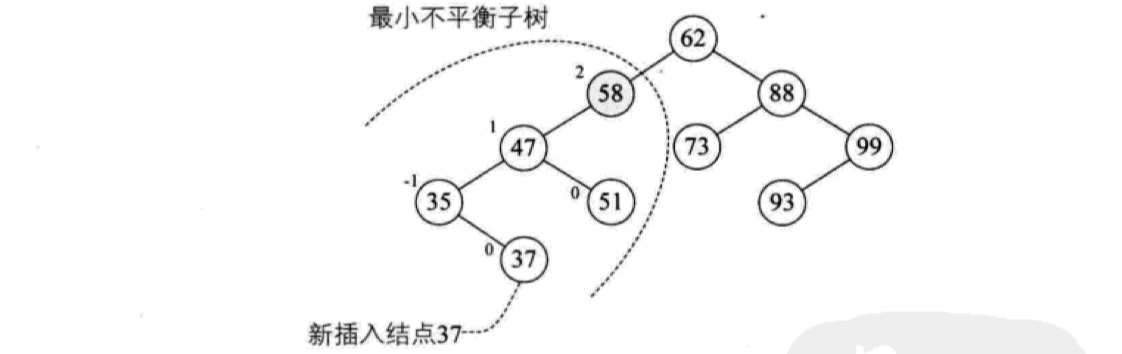
最小不平衡子树
距离插入节点最近的,且平衡因子绝对值大于 1 的节点为根的子树,叫做最小不平衡子树,比如下图中以存储元素 58 的节点为根的子树就是最小不平衡子树:
左旋/右旋操作
所谓左旋和右旋指的是最小不平衡子树旋转的方向。
如果平衡因子小于 -1,即右子树高度值比较大,则需要左旋:
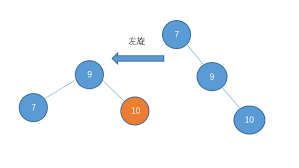
反之,如果平衡因子大于1,即左子树高度值比较大,则需要右旋:
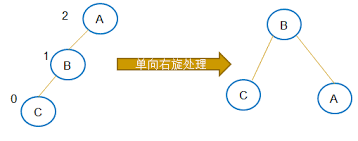
为了方便你理解原理,这里给出的都是最简化的情况,实际处理过程比这个更复杂。
接下来,学院君就来给大家演示如何通过 Go 代码实现平衡二叉树,最后分析下平衡二叉树的算法复杂度。
平衡二叉树的构建过程
在开始之前,我们先通过一个对比来加强理解,在没有介绍平衡二叉树之前,你可能会构造出这样的一棵二叉树:
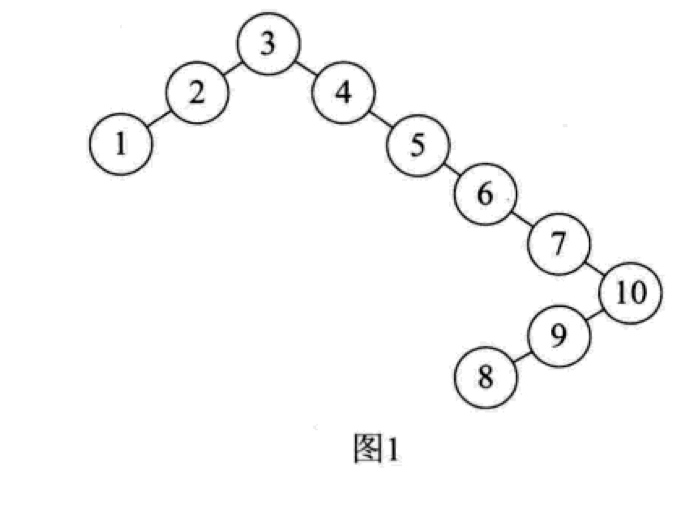
虽然这也是一棵二叉排序树,但是层数达到 8,显然可以通过平衡二叉树来降低层数,提高性能,如果把它转化为平衡二叉树,会是这个样子:
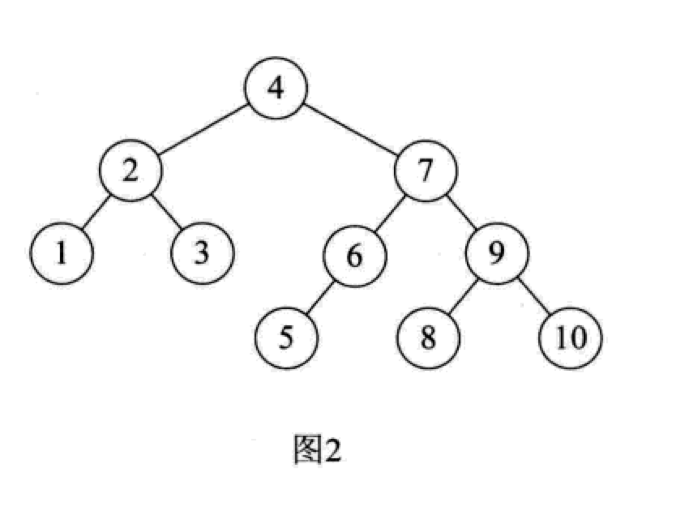
层数降低了一半,变成了 4 层,性能提升了一倍。那么这个平衡二叉树是怎么构建的呢?
假设插入节点的顺序是 {3,2,1,4,5,6,7,10,9,8},两个节点之前不用考虑,我们从第三个节点开始分析:
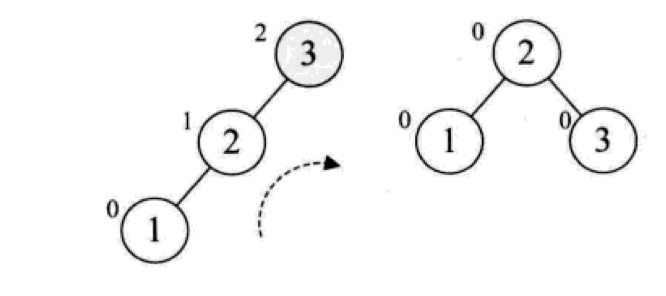
插入第三个节点 1 时,左子树高度是 2,右子树高度是 0,高度差的绝对值是 2,不符合平衡二叉树的要求,需要把以 3 为根节点的子树进行右旋,到右图那个样子,左右子树高度差为 0,符合平衡二叉树要求,完成调整。
同理,插入第四个节点 4 的时候,左右子树高度差为 -1,符合平衡二叉树要求。
继续插入第五个节点,此时又不符合平衡二叉树的要求了,这个时候右子树比较高,需要左旋:
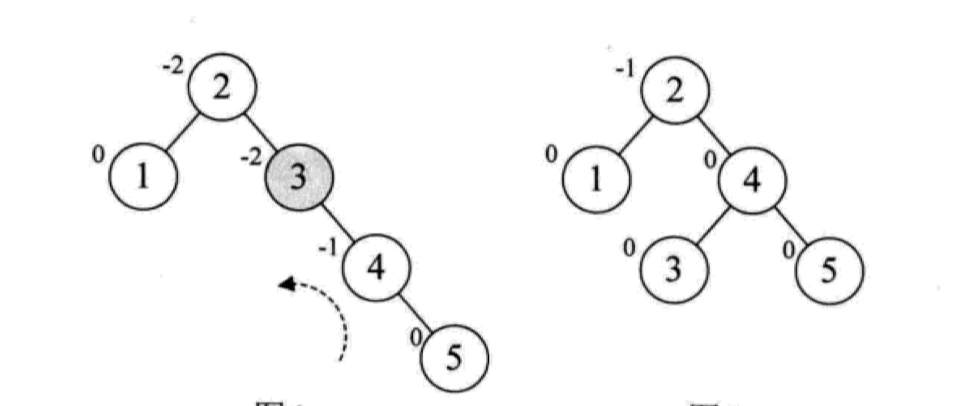
旋转的时候以最小不平衡子树为单位,此时最小的不平衡子树是 3、4、5 三个节点构成的子树,我们以 4 为中心进行左旋,将树结构调整为右图所示的样子,满足了平衡二叉树的要求,停止调整。
注意到我们每次新增节点的时候,会调整以每个节点为根节点的左右子树的高度差,然后从最小子树开始进行调整,直到以每个节点为根节点的子树符合平衡二叉树的要求,这样整棵树就符合平衡二叉树的要求了。
继续增加节点,当插入节点 6 时,发现根节点 2 左右子树的高度差值为 -2,又不满足平衡二叉树了,这个时候,需要以 2 为中心对树进行左旋,最终调整为右图所示的结构满足平衡二叉树要求(右子树中旋转到根节点的节点对应子树需要移到旋转后二叉树的左子树中,以便满足二叉排序树的要求):
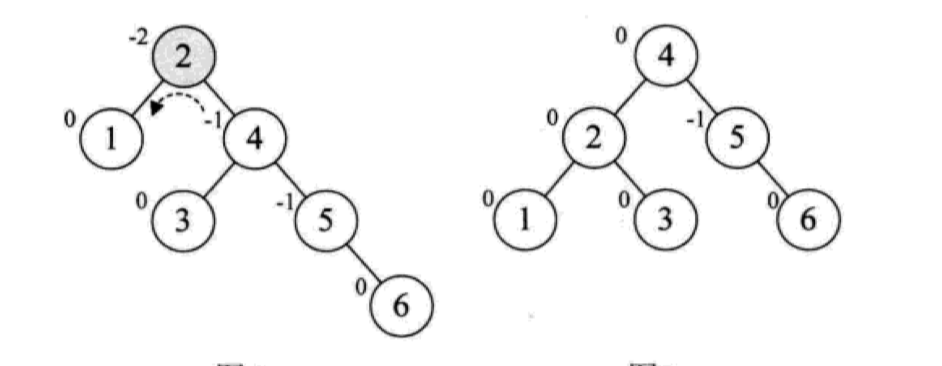
继续增加节点 7,此时以 5 为根节点的最小子树不满足平衡二叉树的要求了,需要左旋:
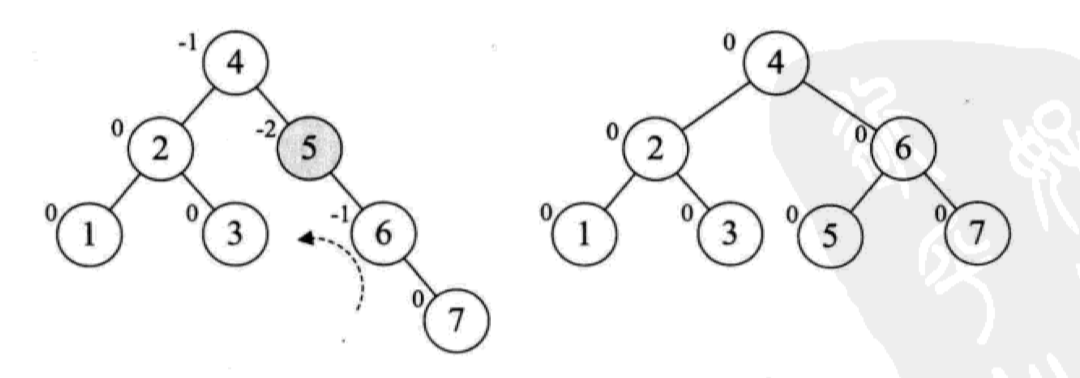
继续增加节点 10,满足平衡二叉树要求,再插入节点 9,又不满足了:
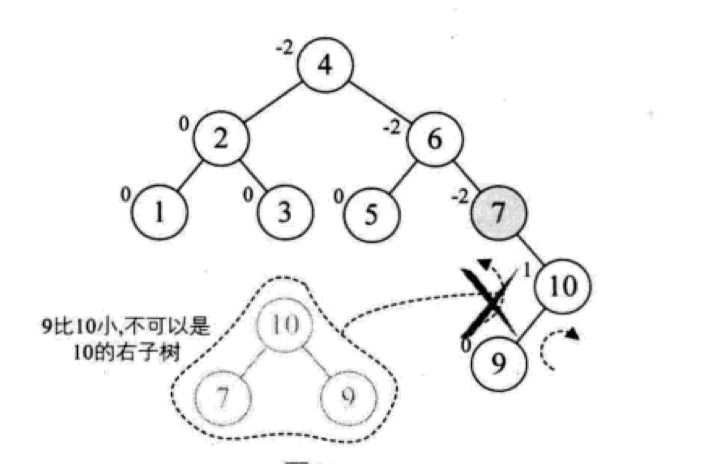
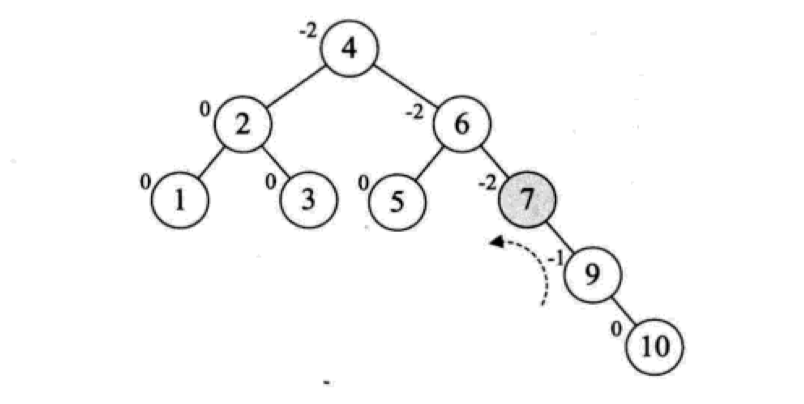
这个时候,情况有点微妙,不像我们之前旋转的时候时候处理情况都比较简单,单纯左转满足不了需求,需要先将以 10 作为根节点的子树做一次右旋,再将以 7 为根节点的子树做一次左旋,才能让这棵不平衡子树转化为平衡子树:
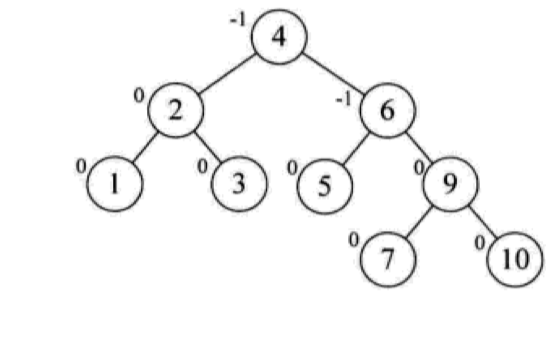
这样整棵二叉树就满足平衡二叉树的要求了:
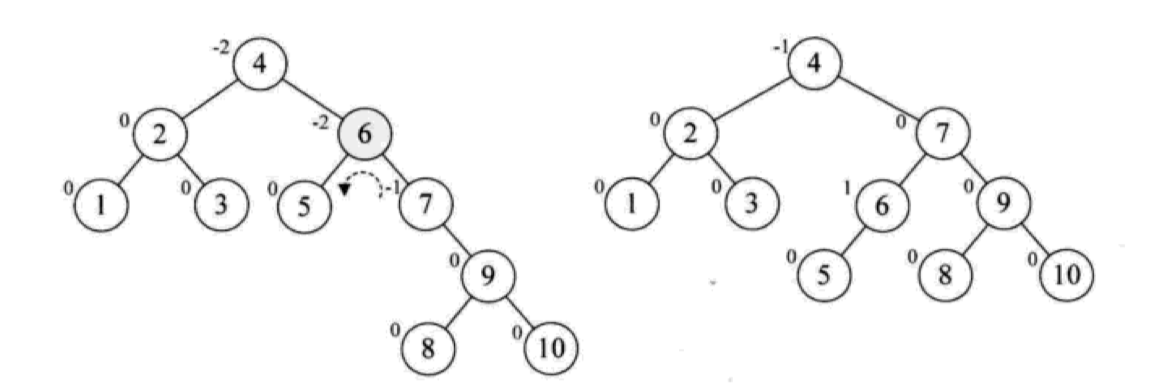
最后,我们插入节点 8,此时情况和刚才类似,这个时候,我们以 9 为根节点对子树进行右旋,再以 6 为根节点对子树进行左旋,最终达到平衡状态:
总结一下,大体的思路是平衡因子 BF 的值大于 1 时,右旋,小于 -1 时左旋,如果最小不平衡子树的 BF 值和其子树的 BF 值符号相反时,需要先将子树进行旋转使两者 BF 值符号相同,再旋转最小不平衡子树。
我们将单纯的左旋、右旋叫做单旋处理,将需要两次旋转处理的操作叫做双旋处理。
下面我们将上面演示的平衡二叉树构建过程转化为 Go 代码实现。
平衡二叉树的实现代码
节点类
我们还是使用二叉链表来实现二叉树的存储,对应的节点类结构体如下:
// AVLNode 平衡二叉树节点类
type AVLNode struct {
Data int
Left, Right *AVLNode
Height int // 以该节点作为根节点对应子树的高度,用于计算平衡因子
}
// AVLTree 平衡二叉树结构体
type AVLTree struct {
root *AVLNode // 根节点
}
// NewAVLTree 平衡二叉树构造函数
func NewAVLTree(data int) *AVLTree {
return &AVLTree{
root: &AVLNode{Data: data, Height: 1},
}
}
和普通二叉树节点相比,新增了一个 Height 属性用于计算平衡因子,平衡二叉树对应的结构体是 AVLTree,我们在其中组合了 AVLNode 指针作为根节点,最后还提供了一个 NewAVLTree 构造函数用于对平衡二叉树进行初始化。
节点查找实现
平衡二叉树也是二叉排序树,所以查找实现和二叉排序差不多,这里我们分别针对 AVLTree 和 AVLNode 提供了 Find 方法,前者作为外部访问入口,后者作为真正实现:
// Find 查找指定节点
func (tree *AVLTree) Find(data int) *AVLNode {
// 空树直接返回空
if tree.root == nil {
return nil
}
return tree.root.Find(data)
}
func (node *AVLNode) Find(data int) *AVLNode {
if data == node.Data {
return node
} else if data < node.Data {
// 如果查找的值小于节点值,从节点的左子树开始查找
if node.Left == nil {
return nil
}
return node.Left.Find(data)
} else {
// 如果查找的值大于节点值,从节点的右子树开始查找
if node.Right == nil {
return nil
}
return node.Right.Find(data)
}
}
节点插入实现
下面我们来实现最关键的节点插入算法,如果你完全理解了上面的平衡二叉树构建过程,则很容易将其翻译成如下 Go 代码实现:
// Insert 插入节点到平衡二叉树
func (tree *AVLTree) Insert(data int) {
// 从根节点开始插入数据
// 根节点在动态变化,所以需要不断刷新
tree.root = tree.root.Insert(data)
}
func (node *AVLNode) Insert(data int) *AVLNode {
// 如果节点为空,则初始化该节点
if node == nil {
return &AVLNode{Data: data, Height: 1}
}
// 如果值重复,则什么都不做
if node.Data == data {
return node
}
// 辅助变量,用于存储(旋转后)子树根节点
var newTreeNode *AVLNode
if data > node.Data {
// 插入的值大于当前节点值,要从右子树插入
node.Right = node.Right.Insert(data)
// 计算插入节点后当前节点的平衡因子
// 按照平衡二叉树的特征,平衡因子绝对值不能大于 1
bf := node.BalanceFactor()
// 如果右子树高度变高了,导致左子树-右子树的高度从 -1 变成了 -2
if bf == -2 {
if data > node.Right.Data {
// 表示在右子树中插入右子节点导致失衡,需要单左旋
newTreeNode = LeftRotate(node)
} else {
// 表示在右子树中插上左子节点导致失衡,需要先右后左双旋
newTreeNode = RightLeftRotation(node)
}
}
} else {
// 插入的值小于当前节点值,要从左子树插入
node.Left = node.Left.Insert(data)
bf := node.BalanceFactor()
// 左子树的高度变高了,导致左子树-右子树的高度从 1 变成了 2
if bf == 2 {
if data < node.Left.Data {
// 表示在左子树中插入左子节点导致失衡,需要单右旋
newTreeNode = RightRotate(node)
} else {
// 表示在左子树中插入右子节点导致失衡,需要先左后右双旋
newTreeNode = LeftRightRotation(node)
}
}
}
if newTreeNode == nil {
// 根节点没变,直接更新子树高度,并返回当前节点指针
node.UpdateHeight()
return node
} else {
// 经过旋转处理后,子树根节点变了,需要更新新的子树高度,然后返回新的子树根节点指针
newTreeNode.UpdateHeight()
return newTreeNode
}
}
// UpdateHeight 更新节点树高度
func (node *AVLNode) UpdateHeight() {
if node == nil {
return
}
// 分别计算左子树和右子树的高度
leftHeight, rightHeight := 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
// 以更高的子树高度作为节点树高度
maxHeight := leftHeight
if rightHeight > maxHeight {
maxHeight = rightHeight
}
// 最终高度要加上节点本身所在的那一层
node.Height = maxHeight + 1
}
// BalanceFactor 计算节点平衡因子(即左右子树的高度差)
func (node *AVLNode) BalanceFactor() int {
leftHeight, rightHeight := 0, 0
if node.Left != nil {
leftHeight = node.Left.Height
}
if node.Right != nil {
rightHeight = node.Right.Height
}
return leftHeight - rightHeight
}
// RightRotate 右旋操作
func RightRotate(node *AVLNode) *AVLNode {
pivot := node.Left // pivot 表示新插入的节点
pivotR := pivot.Right // 暂存 pivot 右子树入口节点
pivot.Right = node // 右旋后最小不平衡子树根节点 node 变成 pivot 的右子节点
node.Left = pivotR // 而 pivot 原本的右子节点需要挂载到 node 节点的左子树上
// 只有 node 和 pivot 的高度改变了
node.UpdateHeight()
pivot.UpdateHeight()
// 返回右旋后的子树根节点指针,即 pivot
return pivot
}
// LeftRotate 左旋操作
func LeftRotate(node *AVLNode) *AVLNode {
pivot := node.Right // pivot 表示新插入的节点
pivotL := pivot.Left // 暂存 pivot 左子树入口节点
pivot.Left = node // 左旋后最小不平衡子树根节点 node 变成 pivot 的左子节点
node.Right = pivotL // 而 pivot 原本的左子节点需要挂载到 node 节点的右子树上
// 只有 node 和 pivot 的高度改变了
node.UpdateHeight()
pivot.UpdateHeight()
// 返回旋后的子树根节点指针,即 pivot
return pivot
}
// LeftRightRotation 双旋操作(先左后右)
func LeftRightRotation(node *AVLNode) *AVLNode {
node.Left = LeftRotate(node.Left)
return RightRotate(node)
}
// RightLeftRotation 先右旋后左旋
func RightLeftRotation(node *AVLNode) *AVLNode {
node.Right = RightRotate(node.Right)
return LeftRotate(node)
}
和查找实现一样,这里定义树和节点级别的 Insert 方法,前者作为外部访问入口,后者定义真正的实现逻辑。这里还定义了其他几个辅助函数来完成平衡二叉树的构建,用于更新节点树高度的 UpdateHeight,用于计算节点平衡因子的 BalanceFactor ,以及用于实现左旋的 LeftRotate,用于实现右旋的 RightRotate,用于实现双旋的 LeftRightRotation 和 RightLeftRotation ,当然,最核心的还是节点类的插入方法实现,这里学院君编写了详细的注释,你可以参照前面的平衡二叉树构建过程图示对比着去理解。
中序遍历平衡二叉树
构建完平衡二叉树后,和二叉排序树一样,可以通过中序遍历对其进行遍历:
// Traverse 中序遍历平衡二叉树
func (tree *AVLTree) Traverse() {
// 从根节点开始遍历
tree.root.Traverse()
}
func (node *AVLNode) Traverse() {
// 节点为空则退出当前递归
if node == nil {
return
}
// 否则先从左子树最左侧节点开始遍历
node.Left.Traverse()
// 打印位于中间的根节点
fmt.Printf("%d(%d) ", node.Data, node.BalanceFactor())
// 最后按照和左子树一样的逻辑遍历右子树
node.Right.Traverse()
}
在打印节点值的时候,还顺便打印了该节点的平衡因子,以便判断是否满足平衡二叉树的特征。
判断是否是平衡二叉树
当然,你也可以单独编写方法来判断一棵树是否是平衡二叉树,调用 AVLTree 类提供的 IsAVLTree 方法即可:
// IsAVLTree 判断是不是平衡二叉树
func (tree *AVLTree) IsAVLTree() bool {
if tree == nil || tree.root == nil {
return true
}
// 判断每个节点是否符合平衡二叉树的定义
if tree.root.IsBalanced() {
return true
}
return false
}
// IsBalanced 判断节点是否符合平衡二叉树的定义
func (node *AVLNode) IsBalanced() bool {
if node == nil {
return true
}
// 左右子树都为空是叶子节点
if node.Left == nil && node.Right == nil {
// 叶子节点高度都是 1
if node.Height == 1 {
return true
} else {
fmt.Println("叶子节点高度值: ", node.Height)
return false
}
} else if node.Left != nil && node.Right != nil {
// 左右子树不为空
// 左子树所有节点值必须比父节点小,右子树所有节点值必须比父节点大(AVL 树首先是二叉排序树)
if node.Left.Data > node.Data || node.Right.Data < node.Data {
// 不符合 AVL 树定义
fmt.Printf("父节点值是 %v, 左子节点值是 %v, 右子节点值是 %v\n", node.Data, node.Left.Data, node.Right.Data)
return false
}
// 计算平衡因子 BF 绝对值
bf := node.Left.Height - node.Right.Height
// 平衡因子不能大于 1
if math.Abs(float64(bf)) > 1 {
fmt.Println("平衡因子 BF 值: ", bf)
return false
}
// 如果左子树比右子树高,那么父节点的高度等于左子树 +1
if node.Left.Height > node.Right.Height {
if node.Height != node.Left.Height+1 {
fmt.Printf("%#v 高度: %v, 左子树高度: %v, 右子树高度: %v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
} else {
// 如果右子树比左子树高,那么父节点的高度等于右子树 +1
if node.Height != node.Right.Height+1 {
fmt.Printf("%#v 高度: %v, 左子树高度: %v, 右子树高度: %v\n", node, node.Height, node.Left.Height, node.Right.Height)
return false
}
}
// 递归判断左子树
if !node.Left.IsBalanced() {
return false
}
// 递归判断右子树
if !node.Right.IsBalanced() {
return false
}
} else {
// 只存在一棵子树
if node.Right != nil {
// 子树高度只能是 1
if node.Right.Height == 1 && node.Right.Left == nil && node.Right.Right == nil {
if node.Right.Data < node.Data {
// 右子节点值必须比父节点值大
fmt.Printf("节点值: %v,(%#v,%#v)", node.Data, node.Right, node.Left)
return false
}
} else {
fmt.Printf("节点值: %v,(%#v,%#v)", node.Data, node.Right, node.Left)
return false
}
} else {
if node.Left.Height == 1 && node.Left.Left == nil && node.Left.Right == nil {
if node.Left.Data > node.Data {
// 左子节点值必须比父节点值小
fmt.Printf("节点值: %v,(%#v,%#v) child", node.Data, node.Right, node.Left)
return false
}
} else {
fmt.Printf("节点值: %v,(%#v,%#v) child", node.Data, node.Right, node.Left)
return false
}
}
}
return true
}
节点删除实现
节点插入的逆操作是节点删除,和节点插入一样,平衡二叉树的节点删除也要不断去判断删除节点后是否还满足平衡二叉树的要求,如果不满足的话同样要做旋转处理,我们可以结合上篇教程介绍的二叉排序树节点删除以及前面的平衡二叉树节点插入实现编写对应的平衡二叉树节点删除实现代码:
// Delete 删除指定节点
func (tree *AVLTree) Delete(data int) {
// 空树直接返回
if tree.root == nil {
return
}
// 删除指定节点,和插入节点一样,根节点也会随着 AVL 树的旋转动态变化
tree.root = tree.root.Delete(data)
}
func (node *AVLNode) Delete(data int) *AVLNode {
// 空节点直接返回 nil
if node == nil {
return nil
}
if data < node.Data {
// 如果删除节点值小于当前节点值,则进入当前节点的左子树删除元素
node.Left = node.Left.Delete(data)
// 删除后要更新左子树高度
node.Left.UpdateHeight()
} else if data > node.Data {
// 如果删除节点值大于当前节点值,则进入当前节点的右子树删除元素
node.Right = node.Right.Delete(data)
// 删除后要更新右子树高度
node.Right.UpdateHeight()
} else {
// 找到待删除节点后
// 第一种情况,删除的节点没有左右子树,直接删除即可
if node.Left == nil && node.Right == nil {
// 返回 nil 表示直接删除该节点
return nil
}
// 第二种情况,待删除节点包含左右子树,选择高度更高的子树下的节点来替换待删除的节点
// 如果左子树更高,选择左子树中值最大的节点,也就是左子树最右边的叶子节点
// 如果右子树更高,选择右子树中值最小的节点,也就是右子树最左边的叶子节点
// 最后,删除这个叶子节点即可
if node.Left != nil && node.Right != nil {
// 左子树更高,拿左子树中值最大的节点替换
if node.Left.Height > node.Right.Height {
maxNode := node.Left
for maxNode.Right != nil {
maxNode = maxNode.Right
}
// 将值最大的节点值赋值给待删除节点
node.Data = maxNode.Data
// 然后把值最大的节点删除
node.Left = node.Left.Delete(maxNode.Data)
// 删除后要更新左子树高度
node.Left.UpdateHeight()
} else {
// 右子树更高,拿右子树中值最小的节点替换
minNode := node.Right
for minNode.Left != nil {
minNode = minNode.Left
}
// 将值最小的节点值赋值给待删除节点
node.Data = minNode.Data
// 然后把值最小的节点删除
node.Right = node.Right.Delete(minNode.Data)
// 删除后要更新右子树高度
node.Right.UpdateHeight()
}
} else {
// 只有左子树或只有右子树
// 只有一棵子树,该子树也只是一个节点,则将该节点值赋值给待删除的节点,然后置子树为空
if node.Left != nil {
// 第三种情况,删除的节点只有左子树
// 根据 AVL 树的特征,可以知道左子树其实就只有一个节点,否则高度差就等于 2 了
node.Data = node.Left.Data
node.Height = 1
node.Left = nil
} else if node.Right != nil {
// 第四种情况,删除的节点只有右子树
// 根据 AVL 树的特征,可以知道右子树其实就只有一个节点,否则高度差就等于 2 了
node.Data = node.Right.Data
node.Height = 1
node.Right = nil
}
}
// 找到指定值对应的待删除节点并进行替换删除后,直接返回该节点
return node
}
// 左右子树递归删除节点后需要平衡
var newNode *AVLNode
// 相当删除了右子树的节点,左边比右边高了,不平衡
if node.BalanceFactor() == 2 {
if node.Left.BalanceFactor() >= 0 {
newNode = RightRotate(node)
} else {
newNode = LeftRightRotation(node)
}
// 相当删除了左子树的节点,右边比左边高了,不平衡
} else if node.BalanceFactor() == -2 {
if node.Right.BalanceFactor() <= 0 {
newNode = LeftRotate(node)
} else {
newNode = RightLeftRotation(node)
}
}
if newNode == nil {
node.UpdateHeight()
return node
} else {
newNode.UpdateHeight()
return newNode
}
}
编写简单的测试代码
至此,我们已经完成了平衡二叉树节点的「增删查」实现代码,最后,我们编写一段简单的测试代码来测试上述代码是否能够正常工作:
func main() {
// 初始化 AVL 树
avlTree := NewAVLTree(3)
// 插入节点
avlTree.Insert(2)
avlTree.Insert(1)
avlTree.Insert(4)
avlTree.Insert(5)
avlTree.Insert(6)
avlTree.Insert(7)
avlTree.Insert(10)
avlTree.Insert(9)
avlTree.Insert(8)
// 判断是否是平衡二叉树
fmt.Print("avlTree 是平衡二叉树: ")
fmt.Println(avlTree.IsAVLTree())
// 中序遍历生成的二叉树看是否是二叉排序树
fmt.Print("中序遍历结果: ")
avlTree.Traverse()
fmt.Println()
// 查找节点
fmt.Print("查找值为 5 的节点: ")
fmt.Printf("%v\n", avlTree.Find(5))
// 删除节点
avlTree.Delete(5)
// 删除后是否还是平衡二叉树
fmt.Print("avlTree 仍然是平衡二叉树: ")
fmt.Println(avlTree.IsAVLTree())
fmt.Print("删除节点后的中序遍历结果: ")
avlTree.Traverse()
fmt.Println()
}
我们以上一篇分享的示例数据为例,通过上述插入节点代码将这些数据插入到二叉树中,看最终生成的二叉树是否是平衡二叉树:

结果符合我们的预期,构建的二叉树和下面这个二叉树一模一样:

说明我们成功构建出了平衡二叉树。
算法复杂度
我们在讲二叉排序树的插入、删除、查找时提到,最理想的情况下,时间复杂度是 O(logn),而平衡二叉树就是这种理想情况,虽然平衡二叉树性能是最好的,也是最稳定的,但是这套算法实现起来比较复杂,每次插入节点和删除节点都需要判断剩下节点构成的二叉排序树是否满足平衡二叉树的要求,如果不满足需要做相应的左旋右旋处理,维护成本高,因此,在工程实践上,我们更多时候使用的是红黑树这种二叉排序树,它是一种不严格的平衡二叉树,实现起来更加简单,性能也接近严格的平衡二叉树,下一篇学院君将会给大家分享这种数据结构及其实现。