KMP 算法可以说是字符串匹配算法中最知名的算法了,KMP 算法是根据三位作者(D.E.Knuth,J.H.Morris 和 V.R.Pratt)的名字来命名的,算法的全称是 Knuth Morris Pratt 算法,简称为 KMP 算法。
核心思想
假设主串是 a,模式串是 b。在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,我们希望找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况,从而避免 BF 算法这种暴力匹配,提高算法性能。下面我们来探讨下这个规律如何找到。
参考下面个主串和模式串的匹配,当模式串移动到当前位置,比对到最后一个字符 D 时,发现与主串不匹配,如果按照 BF 算法,就是把模式串往后移一位,再逐个比较,这样做固然可以,但是效率很差:

一个基本事实是,当 D 与主串不匹配时,我们已知前面的主串序列是 ABCDA,如果把模式串往后移一位肯定和主串不匹配,我们可不可以直接把模式串移到下一个可能和 A 匹配的主串位置?
实际上,KMP 算法正是基于这一理念,设法利用这个已知信息,不把模式串移到已经比较过的位置,继续把它向后移,这样综合下来就极大提高了搜索匹配效率。
怎么找到这个规律,确定把模式串往后移多少位呢?在模式串和主串匹配的过程中,我们把不能匹配的那个字符仍然叫作「坏字符」,把已经匹配的那段字符串叫作「好前缀」:
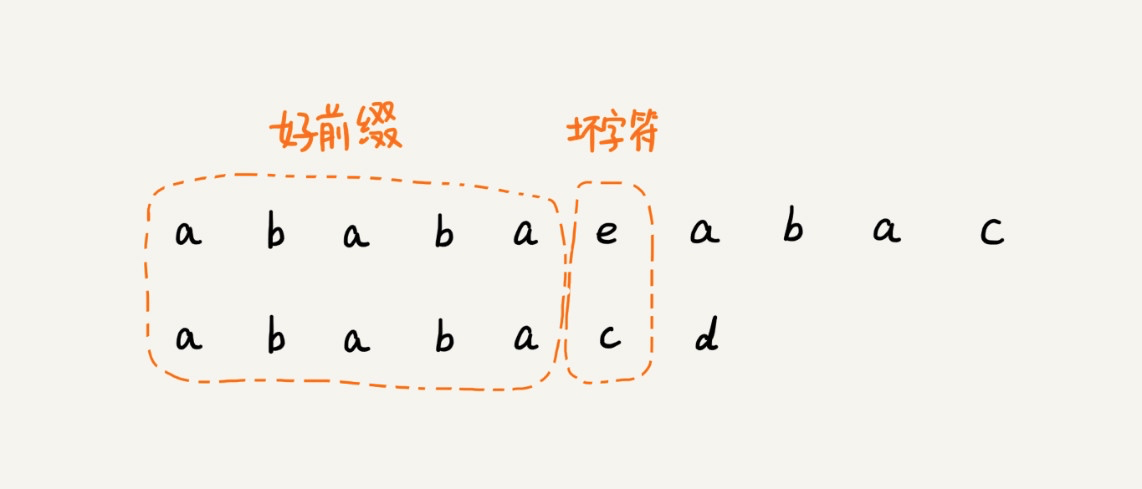
在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,我们只需要拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的下标位置,然后将模式串后移到该位置即可。
这里,我们要解释几个概念:
- 后缀子串:以某个字符串最后一个字符为尾字符的子串(不包含字符串自身),比如上面的
ababa,后缀子串为baba、aba、ba、a; - 前缀子串:以某个字符串第一个字符为首字符的子串(不包含字符串自身),还是以
ababa为例,前缀子串为a、aba、abab; - 最长可匹配后缀子串:后缀子串与前缀子串最长可匹配子串,也可叫做共有子串,以
ababa为例,自然是aba了,长度为 3; - 最长可匹配前缀子串:与上面定义相对,即前缀子串与后缀子串最长可匹配子串。最长可匹配前缀子串和最长可匹配后缀子串肯定是一样的。
假设坏字符所在位置是 j,最长可匹配后缀子串长度为 k,则模式串需要后移的位数为 j-k。每当我们遇到坏字符,就将模式串后移 j-k 位,直到模式串与对应主串字符完全匹配;如果移到最后还是不匹配,则返回 -1。这就是 KMP 算法的核心思想。
实现原理
了解了核心思想,接下来,就可以考虑如何实现 KMP 算法了,实现 KMP 算法最核心的部分是构建一个用来存储模式串中每个前缀子串(这些前缀都有可能是好前缀)最长可匹配前缀子串的结尾字符下标数组,我们把这个数组叫做 next 数组,对于上面 ababacd 这个模式串而言,对应的 next 数组如下:
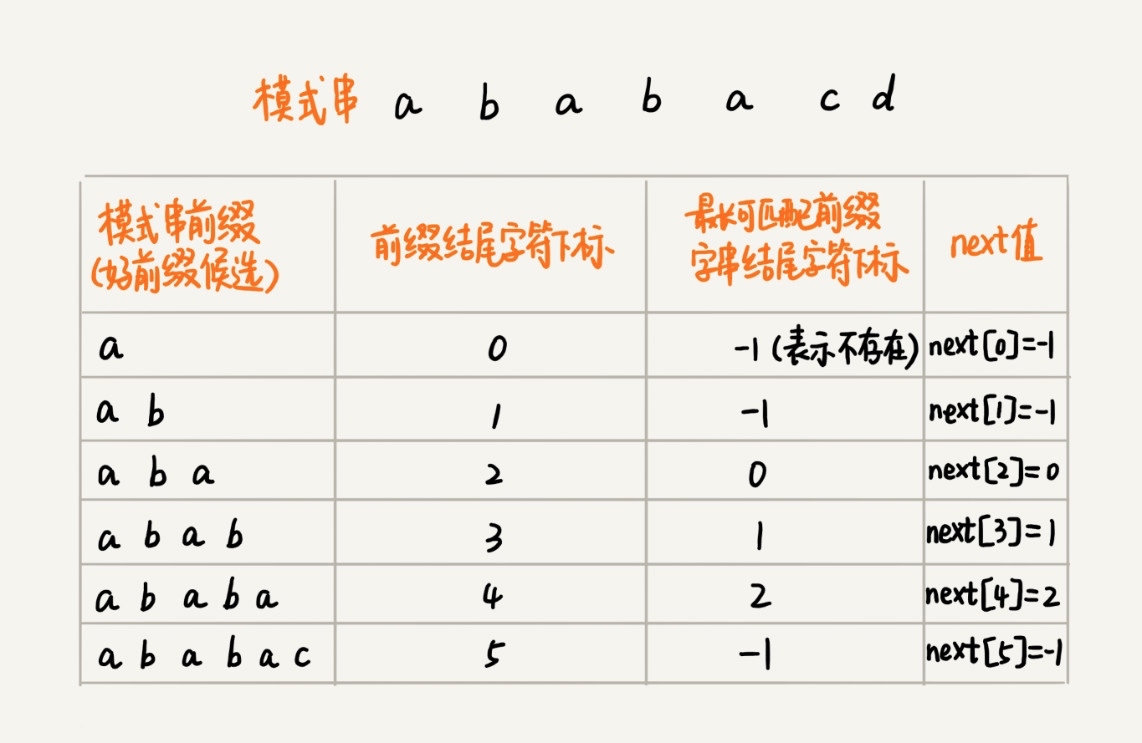
其中,数组的下标是前缀子串结尾字符下标,数组的值是这个前缀的最长可匹配前缀子串的结尾字符下标。
有了这个 next 数组,我们就可以实现 KMP 匹配算法的核心代码了。
示例代码
下面是一个基于 KMP 算法实现的 Golang 版字符串查找函数:
package main
import "fmt"
// 生成 next 数组
func generateNext(p string) []int {
m := len(p)
next := make([]int, m, m)
next[0] = -1
next[1] = 0
i, j := 0, 1 // 前缀子串、后缀子串起始位置
// 因为是通过最长可匹配前缀子串计算,所以 j 的值最大不会超过 m-1
for j < m - 1 {
if i == -1 || p[i] == p[j] {
i++
j++
// 设置当前最长可匹配前缀子串结尾字符下标
next[j] = i
} else {
// 如果 p[i] != p[j],回到上一个最长可匹配前缀子串结尾字符下标
i = next[i]
}
}
return next
}
// KMP 算法实现函数
func kmpSearch(s, p string) int {
n := len(s) // 主串长度
m := len(p) // 模式串长度
next := generateNext(p) // 生成 next 数组
i, j := 0, 0
for i < n && j < m {
// 如果主串字符和模式串字符不相等,
// 更新模式串坏字符下标位置为好前缀最长可匹配前缀子串尾字符下标
// 然后从这个位置重新开始与主串匹配
// 相当于前面提到的把模式串向后移动 j - k 位
if j == -1 || s[i] == p[j] {
i++
j++
} else {
j = next[j]
}
}
if j == m {
// 完全匹配,返回下标位置
return i - j
} else {
return -1
}
}
// 基于 KMP 算法实现查找字符串子串函数
func strStrV2(haystack, needle string) int {
// 子串长度=0
if len(needle) == 0 {
return 0
}
//主串长度=0,或者主串长度小于子串长度
if len(haystack) == 0 || len(haystack) < len(needle) {
return -1
}
// 子串长度=1时单独判断
if len(needle) == 1 {
i := 0
for ; i < len(haystack); i++ {
if haystack[i] == needle[0] {
return i
}
}
return -1
}
// 其他情况走 KMP 算法
return kmpSearch(haystack, needle)
}
func main() {
s := "Hello, 学院君!"
p := "学院君"
pos := strStrV2(s, p)
fmt.Printf("Find \"%s\" at %d in \"%s\"\n", p, pos, s)
}
运行上述代码,打印结果如下,说明字符串查找函数可以正常工作:

性能分析
KMP 算法比 BF 算法实现起来要复杂的多,不过带来的好处是执行效率的提升,综合 KMP 算法实现函数和 next 数组生成函数,它的时间复杂度是 O(n+m),其中 n 是主串长度,m 是子串长度,m 和 n 的值越大,性能比 BF 算法更好,考虑到对于较长的主串,m 相对于 n 而言一般可以忽略,所以可以把 KMP 算法的时间复杂度近似看作 O(n)。
这个性能还是相当不错的,因此,KMP 算法被广泛用于字符串查找和匹配场景。




弱弱的问一下生成 next 数组的函数 generateNext 是不是有问题,试了下文中的”ababacd”,输出结果[-1 0 0 1 2 3 0],我哪里理解错了的话麻烦给指点一下[呲牙][呲牙][呲牙]