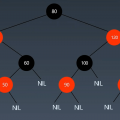
上篇教程学院君给大家介绍了红黑树的由来和特性,今天这篇教程我们一起来看下红黑树是如何维护自平衡的,包括节点插入、删除和对应的实现代码。
插入节点
红黑树规定,插入的节点必须是红色的,而且,二叉排序(查找)树中新插入的节点都是放在叶子节点上。在此前提下,我们来看两种最简单的情况:
- 如果插入节点的父节点是黑色的,那我们什么都不用做,它仍然满足红黑树的定义。
- 如果插入的节点是根节点,那我们直接把它设置为黑色就可以了。
除此之外,其他情况都会违背红黑树的特性,所以我们需要进行动态调整,与平衡二叉树不同,调整的过程除了左右旋转之外,还涉及到节点颜色的调整。
新节点插入之后,如果红黑树的平衡被打破,那一般会有下面三种情况,我们只需要根据每种情况的特点,不停地调整,就可以让红黑树继续符合定义,也就是继续保持平衡:
有了前面平衡二叉树的铺垫,相信理解起来红黑树的构建过程将会更加轻松。为了方便表述,我们把正在处理的节点叫关注节点。
CASE 1:如果关注节点是 a(待插入节点),它的叔叔节点(父亲的兄弟节点,从二叉排序树的角度来说叫伯伯节点更合适?) d 是红色,我们就依次执行下面的操作:
- 将关注节点
a的父节点b、叔叔节点d的颜色都设置成黑色; - 将关注节点
a的祖父节点c的颜色设置成红色; - 关注节点变成
a的祖父节点c; - 跳到下面的 CASE 2 或者 CASE 3 继续处理。

CASE 2:如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的右子节点,我们就依次执行下面的操作:
- 关注节点变成节点
a的父节点b; - 围绕新的关注节点
b左旋; - 跳到 CASE 3。

CASE 3:如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的左子节点,我们就依次执行下面的操作:
- 围绕关注节点
a的祖父节点c右旋; - 将关注节点
a的父节点b、兄弟节点c的颜色互换。 - 调整结束,至此就构造出来一棵红黑树。

学院君注:在看上面三个 CASE 的时候要动态的去看,从 CASE 1 跳到 CASE 2 或 CASE 3,或者从 CASE 2 跳到 CASE 3,或者从 CASE 3 开始,不要分割开来。如果从 CASE 1 跳到到 CASE 2 或 CASE 3,后两者的关注节点
a就是 CASE 1 中最终的关注节点c。
删除节点
删除节点的平衡调整更加复杂,可以分为两步,第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后,仍然满足最后一条定义的要求,也就是说,每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;第二步是针对关注节点进行二次调整,让它满足红黑树的第三条定义,即不存在相邻的两个红色节点。
针对删除节点的初步调整
这里需要注意一下,红黑树的定义中「只包含红色节点和黑色节点」,经过初步调整之后,为了保证满足红黑树定义的最后一条要求,有些节点会被标记成两种颜色,「红-黑」或者「黑-黑」。如果一个节点被标记为了「黑-黑」,那在计算黑色节点个数的时候,要算成两个黑色节点。
CASE 1:如果要删除的节点是 a,它只有一个子节点 b,那我们就依次进行下面的操作:
- 删除节点
a,并且把节点b替换到节点a的位置,这一部分操作跟普通的二叉查找树的删除操作一样; - 节点
a只能是黑色,节点b也只能是红色,其他情况均不符合红黑树的定义。这种情况下,我们把节点b改为黑色; - 调整结束,不需要进行二次调整。

CASE 2:如果要删除的节点 a 有两个非空子节点,并且它的后继节点就是节点 a 的右子节点 c
- 如果节点
a的后继节点就是右子节点c,那右子节点c肯定没有左子树(否则就不是后继节点了)。我们把节点a删除,并且将节点c替换到节点a的位置。这一部分操作跟普通的二叉查找树的删除操作无异; - 然后把节点
c的颜色设置为跟节点a相同的颜色; - 如果节点
c是黑色,为了不违反红黑树的最后一条定义,我们给节点c的右子节点d多加一个黑色,这个时候节点d就成了「红-黑」或者「黑-黑」; - 这个时候,关注节点变成了节点
d,第二步的调整操作就会针对关注节点来做。

CASE 3:如果要删除的是节点 a,它有两个非空子节点,并且节点 a 的后继节点不是右子节点,我们就依次进行下面的操作:
- 找到后继节点
d,并将它删除,删除后继节点d的过程参照 CASE 1; - 将节点
a替换成后继节点d; - 把节点
d的颜色设置为跟节点a相同的颜色; - 如果节点
d是黑色,为了不违反红黑树的最后一条定义,我们给节点d的右子节点c多加一个黑色,这个时候节点c就成了「红-黑」或者「黑-黑」; - 这个时候,关注节点变成了节点
c,第二步的调整操作就会针对关注节点来做。

针对关注节点的二次调整
经过初步调整之后,关注节点变成了「红-黑」或者「黑-黑」节点。针对这个关注节点,我们再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。
CASE 1:如果关注节点是 a,它的兄弟节点 c 是红色的
- 围绕关注节点
a的父节点b左旋; - 关注节点
a的父节点b和祖父节点c交换颜色; - 关注节点不变;
- 继续从四种情况中选择适合的规则来调整。

CASE 2:如果关注节点是 a,它的兄弟节点 c 是黑色的,并且节点 c 的左右子节点 d、e 都是黑色的
- 将关注节点
a的兄弟节点c的颜色变成红色; - 从关注节点
a中去掉一个黑色,这个时候节点a就是单纯的红色或者黑色; - 给关注节点
a的父节点b添加一个黑色,这个时候节点b就变成了「红-黑」或者「黑-黑」; - 关注节点从
a变成其父节点b; - 继续从四种情况中选择符合的规则来调整。

CASE 3:如果关注节点是 a,它的兄弟节点 c 是黑色,c 的左子节点 d 是红色,c 的右子节点 e 是黑色,我们就依次进行下面的操作:
- 围绕关注节点
a的兄弟节点c右旋; - 节点
c和节点d交换颜色; - 关注节点不变;
- 跳转到 CASE 4,继续调整。

CASE 4:如果关注节点 a 的兄弟节点 c 是黑色的,并且 c 的右子节点是红色的,我们就依次进行下面的操作:
- 围绕关注节点
a的父节点b左旋; - 将关注节点
a的兄弟节点c的颜色,跟关注节点a的父节点b设置成相同的颜色; - 将关注节点
a的父节点b的颜色设置为黑色; - 从关注节点
a中去掉一个黑色,节点a就变成了单纯的红色或者黑色; - 将关注节点
a的叔叔节点e设置为黑色; - 调整结束。

为什么叶子节点都是黑色的空节点
你可能会好奇,为什么叶子节点都是黑色的空节点,其实这就是为了红黑树实现起来更方便。只要满足这一条要求,那在任何时刻,红黑树的平衡操作都可以归结为我们刚刚讲的那几种情况。
不要担心这么做会浪费存储空间,因为其实只要一个空节点就好了:

以上红黑树的动态平衡过程主要参考了极客时间王争的算法专栏相应教程。
实现代码
定义节点类型及相关方法
package redblacktree
import "fmt"
type color bool
const (
black, red color = true, false
)
// Node is a single element within the tree
type Node struct {
Key interface{}
Value interface{}
color color
Left *Node
Right *Node
Parent *Node
}
func (node *Node) String() string {
return fmt.Sprintf("%v", node.Key)
}
// Size returns the number of elements stored in the subtree.
// Computed dynamically on each call, i.e. the subtree is traversed to count the number of the nodes.
func (node *Node) Size() int {
if node == nil {
return 0
}
size := 1
if node.Left != nil {
size += node.Left.Size()
}
if node.Right != nil {
size += node.Right.Size()
}
return size
}
// 祖父节点
func (node *Node) grandparent() *Node {
if node != nil && node.Parent != nil {
return node.Parent.Parent
}
return nil
}
// 叔伯节点
func (node *Node) uncle() *Node {
if node == nil || node.Parent == nil || node.Parent.Parent == nil {
return nil
}
return node.Parent.sibling()
}
// 兄弟节点
func (node *Node) sibling() *Node {
if node == nil || node.Parent == nil {
return nil
}
if node == node.Parent.Left {
return node.Parent.Right
}
return node.Parent.Left
}
func (node *Node) maximumNode() *Node {
if node == nil {
return nil
}
for node.Right != nil {
node = node.Right
}
return node
}
func (node *Node) output(prefix string, isTail bool, str *string) {
if node.Right != nil {
newPrefix := prefix
if isTail {
newPrefix += "│ "
} else {
newPrefix += " "
}
node.Right.output(newPrefix, false, str)
}
*str += prefix
if isTail {
*str += "└── "
} else {
*str += "┌── "
}
*str += node.String() + "\n"
if node.Left != nil {
newPrefix := prefix
if isTail {
newPrefix += " "
} else {
newPrefix += "│ "
}
node.Left.output(newPrefix, true, str)
}
}
func nodeColor(node *Node) color {
if node == nil {
return black
}
return node.color
}
定义迭代器类型及相关方法
package redblacktree
// Iterator holding the iterator's state
type Iterator struct {
tree *Tree
node *Node
position position
}
type position byte
const (
begin, between, end position = 0, 1, 2
)
// Next moves the iterator to the next element and returns true if there was a next element in the container.
// If Next() returns true, then next element's key and value can be retrieved by Key() and Value().
// If Next() was called for the first time, then it will point the iterator to the first element if it exists.
// Modifies the state of the iterator.
func (iterator *Iterator) Next() bool {
if iterator.position == end {
goto end
}
if iterator.position == begin {
left := iterator.tree.Left()
if left == nil {
goto end
}
iterator.node = left
goto between
}
if iterator.node.Right != nil {
iterator.node = iterator.node.Right
for iterator.node.Left != nil {
iterator.node = iterator.node.Left
}
goto between
}
for iterator.node.Parent != nil {
node := iterator.node
iterator.node = iterator.node.Parent
if node == iterator.node.Left {
goto between
}
}
end:
iterator.node = nil
iterator.position = end
return false
between:
iterator.position = between
return true
}
// Prev moves the iterator to the previous element and returns true if there was a previous element in the container.
// If Prev() returns true, then previous element's key and value can be retrieved by Key() and Value().
// Modifies the state of the iterator.
func (iterator *Iterator) Prev() bool {
if iterator.position == begin {
goto begin
}
if iterator.position == end {
right := iterator.tree.Right()
if right == nil {
goto begin
}
iterator.node = right
goto between
}
if iterator.node.Left != nil {
iterator.node = iterator.node.Left
for iterator.node.Right != nil {
iterator.node = iterator.node.Right
}
goto between
}
for iterator.node.Parent != nil {
node := iterator.node
iterator.node = iterator.node.Parent
if node == iterator.node.Right {
goto between
}
}
begin:
iterator.node = nil
iterator.position = begin
return false
between:
iterator.position = between
return true
}
// Value returns the current element's value.
// Does not modify the state of the iterator.
func (iterator *Iterator) Value() interface{} {
return iterator.node.Value
}
// Key returns the current element's key.
// Does not modify the state of the iterator.
func (iterator *Iterator) Key() interface{} {
return iterator.node.Key
}
// Node returns the current element's node.
// Does not modify the state of the iterator.
func (iterator *Iterator) Node() *Node {
return iterator.node
}
// Begin resets the iterator to its initial state (one-before-first)
// Call Next() to fetch the first element if any.
func (iterator *Iterator) Begin() {
iterator.node = nil
iterator.position = begin
}
// End moves the iterator past the last element (one-past-the-end).
// Call Prev() to fetch the last element if any.
func (iterator *Iterator) End() {
iterator.node = nil
iterator.position = end
}
// First moves the iterator to the first element and returns true if there was a first element in the container.
// If First() returns true, then first element's key and value can be retrieved by Key() and Value().
// Modifies the state of the iterator
func (iterator *Iterator) First() bool {
iterator.Begin()
return iterator.Next()
}
// Last moves the iterator to the last element and returns true if there was a last element in the container.
// If Last() returns true, then last element's key and value can be retrieved by Key() and Value().
// Modifies the state of the iterator.
func (iterator *Iterator) Last() bool {
iterator.End()
return iterator.Prev()
}
定义红黑树实现代码
红黑树是二叉排序(查找)树的一种实现,所以我们先定义一个二叉树的接口:
package tree
type Tree interface {
Empty() bool
Size() int
Clear()
Values() []interface{}
String() string
}
然后以红黑树的形式实现这个接口:
package redblacktree
import (
"github.com/geekr-dev/go-algorithms/tree"
)
// Assert Tree implementation
var _ tree.Tree = (*Tree)(nil)
type Comparator func(a, b interface{}) int
// Tree holds elements of the red-black tree
type Tree struct {
Root *Node
size int
Comparator Comparator
}
// NewTree instantiates a red-black tree with the custom comparator.
func NewTree(comparator Comparator) *Tree {
return &Tree{Comparator: comparator}
}
// Empty returns true if tree does not contain any nodes
func (tree *Tree) Empty() bool {
return tree.size == 0
}
// Size returns number of nodes in the tree.
func (tree *Tree) Size() int {
return tree.size
}
// Get searches the node in the tree by key and returns its node or nil if key is not found in tree.
// Key should adhere to the comparator's type assertion, otherwise method panics.
func (tree *Tree) Get(key interface{}) *Node {
return tree.lookup(key)
}
func (tree *Tree) lookup(key interface{}) *Node {
node := tree.Root
for node != nil {
compare := tree.Comparator(key, node.Key)
switch {
case compare == 0:
return node
case compare < 0:
node = node.Left
case compare > 0:
node = node.Right
}
}
return nil
}
// Iterator returns a stateful iterator whose elements are key/value pairs.
func (tree *Tree) Iterator() Iterator {
return Iterator{tree: tree, node: nil, position: begin}
}
// Keys returns all keys in-order
func (tree *Tree) Keys() []interface{} {
keys := make([]interface{}, tree.size)
it := tree.Iterator()
for i := 0; it.Next(); i++ {
keys[i] = it.Key()
}
return keys
}
// Values returns all values in-order based on the key.
func (tree *Tree) Values() []interface{} {
values := make([]interface{}, tree.size)
it := tree.Iterator()
for i := 0; it.Next(); i++ {
values[i] = it.Value()
}
return values
}
// Clear removes all nodes from the tree.
func (tree *Tree) Clear() {
tree.Root = nil
tree.size = 0
}
// String returns a string representation of tree
func (tree *Tree) String() string {
str := "RedBlackTree\n"
if !tree.Empty() {
tree.Root.output("", true, &str)
}
return str
}
// Left returns the left-most (min) node or nil if tree is empty.
func (tree *Tree) Left() *Node {
var parent *Node
current := tree.Root
for current != nil {
parent = current
current = current.Left
}
return parent
}
// Right returns the right-most (max) node or nil if tree is empty.
func (tree *Tree) Right() *Node {
var parent *Node
current := tree.Root
for current != nil {
parent = current
current = current.Right
}
return parent
}
// Insert 插入新节点到红黑树
// Key should adhere to the comparator's type assertion, otherwise method panics.
func (tree *Tree) Insert(key interface{}, value interface{}) {
var insertedNode *Node
if tree.Root == nil {
// Assert key is of comparator's type for initial tree
tree.Comparator(key, key)
tree.Root = &Node{Key: key, Value: value, color: red}
insertedNode = tree.Root
} else {
node := tree.Root
loop := true
for loop {
compare := tree.Comparator(key, node.Key)
switch {
case compare == 0:
node.Key = key
node.Value = value
return
case compare < 0:
if node.Left == nil {
node.Left = &Node{Key: key, Value: value, color: red}
insertedNode = node.Left
loop = false
} else {
node = node.Left
}
case compare > 0:
if node.Right == nil {
node.Right = &Node{Key: key, Value: value, color: red}
insertedNode = node.Right
loop = false
} else {
node = node.Right
}
}
}
insertedNode.Parent = node
}
tree.insertCase1(insertedNode)
tree.size++
}
// Delete 从红黑树删除节点
// Key should adhere to the comparator's type assertion, otherwise method panics.
func (tree *Tree) Delete(key interface{}) {
var child *Node
node := tree.lookup(key)
if node == nil {
return
}
if node.Left != nil && node.Right != nil {
pred := node.Left.maximumNode()
node.Key = pred.Key
node.Value = pred.Value
node = pred
}
if node.Left == nil || node.Right == nil {
if node.Right == nil {
child = node.Left
} else {
child = node.Right
}
if node.color == black {
node.color = nodeColor(child)
tree.deleteCase1(node)
}
tree.replaceNode(node, child)
if node.Parent == nil && child != nil {
child.color = black
}
}
tree.size--
}
// 左旋
func (tree *Tree) rotateLeft(node *Node) {
right := node.Right
tree.replaceNode(node, right)
node.Right = right.Left
if right.Left != nil {
right.Left.Parent = node
}
right.Left = node
node.Parent = right
}
// 右旋
func (tree *Tree) rotateRight(node *Node) {
left := node.Left
tree.replaceNode(node, left)
node.Left = left.Right
if left.Right != nil {
left.Right.Parent = node
}
left.Right = node
node.Parent = left
}
// 替换节点
func (tree *Tree) replaceNode(old *Node, new *Node) {
if old.Parent == nil {
tree.Root = new
} else {
if old == old.Parent.Left {
old.Parent.Left = new
} else {
old.Parent.Right = new
}
}
if new != nil {
new.Parent = old.Parent
}
}
// 插入的是根节点,直接设置为黑色即可
func (tree *Tree) insertCase1(node *Node) {
if node.Parent == nil {
node.color = black
} else {
tree.insertCase2(node)
}
}
// 父节点是黑色的,什么也不用做
func (tree *Tree) insertCase2(node *Node) {
if nodeColor(node.Parent) == black {
return
}
tree.insertCase3(node)
}
// 对应上述插入节点CASE1
func (tree *Tree) insertCase3(node *Node) {
uncle := node.uncle()
if nodeColor(uncle) == red {
node.Parent.color = black
uncle.color = black
node.grandparent().color = red
tree.insertCase1(node.grandparent())
} else {
tree.insertCase4(node)
}
}
// 对应上述插入节点CASE2
func (tree *Tree) insertCase4(node *Node) {
grandparent := node.grandparent()
if node == node.Parent.Right && node.Parent == grandparent.Left {
tree.rotateLeft(node.Parent)
node = node.Left
} else if node == node.Parent.Left && node.Parent == grandparent.Right {
tree.rotateRight(node.Parent)
node = node.Right
}
tree.insertCase5(node)
}
// 对应上述插入节点CASE3,完成这一步后,红黑树将实现节点插入的自平衡
func (tree *Tree) insertCase5(node *Node) {
node.Parent.color = black
grandparent := node.grandparent()
grandparent.color = red
if node == node.Parent.Left && node.Parent == grandparent.Left {
tree.rotateRight(grandparent)
} else if node == node.Parent.Right && node.Parent == grandparent.Right {
tree.rotateLeft(grandparent)
}
}
// 如果是根节点,则直接删除,不做其他操作,否则进入CASE2
func (tree *Tree) deleteCase1(node *Node) {
if node.Parent == nil {
return
}
tree.deleteCase2(node)
}
// 待删除节点兄弟节点是红色,将父节点标红,兄弟节点标黑
// 如果待删除节点为左子节点,则将父节点左旋,否则右旋,进入CASE3
func (tree *Tree) deleteCase2(node *Node) {
sibling := node.sibling()
if nodeColor(sibling) == red {
node.Parent.color = red
sibling.color = black
if node == node.Parent.Left {
tree.rotateLeft(node.Parent)
} else {
tree.rotateRight(node.Parent)
}
}
tree.deleteCase3(node)
}
// 如果父节点和兄弟节点以及兄弟节点的子节点都是黑色,则调到CASE1,关注节点调整为父节点
// 否则进入CASE4
func (tree *Tree) deleteCase3(node *Node) {
sibling := node.sibling()
if nodeColor(node.Parent) == black &&
nodeColor(sibling) == black &&
nodeColor(sibling.Left) == black &&
nodeColor(sibling.Right) == black {
sibling.color = red
tree.deleteCase1(node.Parent)
} else {
tree.deleteCase4(node)
}
}
// 如果父节点是红色,兄弟节点及其子节点都是黑色,将兄弟节点标红,父节点标黑,完成红黑树自平衡
// 否则进入 CASE5
func (tree *Tree) deleteCase4(node *Node) {
sibling := node.sibling()
if nodeColor(node.Parent) == red &&
nodeColor(sibling) == black &&
nodeColor(sibling.Left) == black &&
nodeColor(sibling.Right) == black {
sibling.color = red
node.Parent.color = black
} else {
tree.deleteCase5(node)
}
}
// 如果待删除节点是父节点的左子节点,且兄弟节点及其右子节点是黑色,左子节点红色,则交换兄弟节点及其左子节点颜色,然后沿着兄弟节点右旋
// 否则交换兄弟节点及其右子节点颜色,沿着兄弟节点做左旋操作
// 进入 CASE6
func (tree *Tree) deleteCase5(node *Node) {
sibling := node.sibling()
if node == node.Parent.Left &&
nodeColor(sibling) == black &&
nodeColor(sibling.Left) == red &&
nodeColor(sibling.Right) == black {
sibling.color = red
sibling.Left.color = black
tree.rotateRight(sibling)
} else if node == node.Parent.Right &&
nodeColor(sibling) == black &&
nodeColor(sibling.Right) == red &&
nodeColor(sibling.Left) == black {
sibling.color = red
sibling.Right.color = black
tree.rotateLeft(sibling)
}
tree.deleteCase6(node)
}
// 最终完成红黑树删除节点后的自平衡
func (tree *Tree) deleteCase6(node *Node) {
sibling := node.sibling()
sibling.color = nodeColor(node.Parent)
node.Parent.color = black
if node == node.Parent.Left && nodeColor(sibling.Right) == red {
sibling.Right.color = black
tree.rotateLeft(node.Parent)
} else if nodeColor(sibling.Left) == red {
sibling.Left.color = black
tree.rotateRight(node.Parent)
}
}
编写测试代码
package redblacktree_test
import (
"fmt"
"testing"
"github.com/geekr-dev/go-algorithms/tree/redblacktree"
)
// IntComparator provides a basic comparison on int
func IntComparator(a, b interface{}) int {
aAsserted := a.(int)
bAsserted := b.(int)
switch {
case aAsserted > bAsserted:
return 1
case aAsserted < bAsserted:
return -1
default:
return 0
}
}
func TestRedBlackTreePut(t *testing.T) {
tree := redblacktree.NewTree(IntComparator)
tree.Insert(5, "e")
tree.Insert(6, "f")
tree.Insert(7, "g")
tree.Insert(3, "c")
tree.Insert(4, "d")
tree.Insert(1, "x")
tree.Insert(2, "b")
tree.Insert(1, "a") // overwrite
if actualValue := tree.Size(); actualValue != 7 {
t.Errorf("Got %v expected %v", actualValue, 7)
}
if actualValue, expectedValue := fmt.Sprintf("%d%d%d%d%d%d%d", tree.Keys()...), "1234567"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if actualValue, expectedValue := fmt.Sprintf("%s%s%s%s%s%s%s", tree.Values()...), "abcdefg"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
tests1 := [][]interface{}{
{1, "a"},
{2, "b"},
{3, "c"},
{4, "d"},
{5, "e"},
{6, "f"},
{7, "g"},
{8, nil},
}
for _, test := range tests1 {
// retrievals
actualNode := tree.Get(test[0])
if actualNode != nil && actualNode.Value != test[1] {
t.Errorf("Got %v expected %v", actualNode.Value, test[1])
}
}
}
func TestRedBlackTreeDelete(t *testing.T) {
tree := redblacktree.NewTree(IntComparator)
tree.Insert(5, "e")
tree.Insert(6, "f")
tree.Insert(7, "g")
tree.Insert(3, "c")
tree.Insert(4, "d")
tree.Insert(1, "x")
tree.Insert(2, "b")
tree.Insert(1, "a") // overwrite
tree.Delete(5)
tree.Delete(6)
tree.Delete(7)
tree.Delete(8)
tree.Delete(5)
if actualValue, expectedValue := fmt.Sprintf("%d%d%d%d", tree.Keys()...), "1234"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if actualValue, expectedValue := fmt.Sprintf("%s%s%s%s", tree.Values()...), "abcd"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if actualValue, expectedValue := fmt.Sprintf("%s%s%s%s", tree.Values()...), "abcd"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if actualValue := tree.Size(); actualValue != 4 {
t.Errorf("Got %v expected %v", actualValue, 7)
}
tests2 := [][]interface{}{
{1, "a"},
{2, "b"},
{3, "c"},
{4, "d"},
{5, nil},
{6, nil},
{7, nil},
{8, nil},
}
for _, test := range tests2 {
actualNode := tree.Get(test[0])
if actualNode != nil && actualNode.Value != test[1] {
t.Errorf("Got %v expected %v", actualNode.Value, test[1])
}
}
tree.Delete(1)
tree.Delete(4)
tree.Delete(2)
tree.Delete(3)
tree.Delete(2)
tree.Delete(2)
if actualValue, expectedValue := fmt.Sprintf("%s", tree.Keys()), "[]"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if actualValue, expectedValue := fmt.Sprintf("%s", tree.Values()), "[]"; actualValue != expectedValue {
t.Errorf("Got %v expected %v", actualValue, expectedValue)
}
if empty, size := tree.Empty(), tree.Size(); empty != true || size != -0 {
t.Errorf("Got %v expected %v", empty, true)
}
}
完整代码看这里:https://github.com/geekr-dev/go-algorithms/tree/master/tree/redblacktree,以上代码引用了 https://github.com/emirpasic/gods 的红黑树实现,结构上略微做了调整,此外,Linux 内核也大量使用了红黑树,对应的 C 实现代码位于 linux/lib/rbtree.c。