前面已经介绍了二叉树的存储和遍历,今天这篇教程我们以二叉排序树为例,来演示如何对二叉树的节点进行「增删改查」。开始之前,我们先来介绍什么是二叉排序树,以及为什么要引入这种二叉树。
什么是二叉排序树
我们前面已经介绍了很多数据结构,比如数组、链表、哈希表等,数组查找性能高,但是插入、删除性能差,链表插入、删除性能高,但查找性能差,哈希表的插入、删除、查找性能都很高,但前提是没有哈希冲突,此外,哈希表存储的数据是无序的,哈希表的扩容非常麻烦,涉及到哈希冲突时,性能不稳定,另外,哈希表用起来爽,构造起来可不简单,要考虑哈希函数的设计、哈希冲突的解决、扩容缩容等一系列问题。
有没有一种插入、删除、查找性能都不错,构建起来也不是很复杂,性能还很稳定的数据结构呢?这就是我们今天要介绍的数据结构 —— 二叉排序树。
二叉排序树也叫二叉搜索树、二叉查找树,简称 BST(Binary Search/Sort Tree)树,它是一种特殊的二叉树,我们重点关注「排序」二字,二叉排序树要求在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值,所以这么看来,二叉排序树是天然有序的。如果按照上篇教程讲的中序遍历,得到的结果将是一个从小到大的有序数据集:
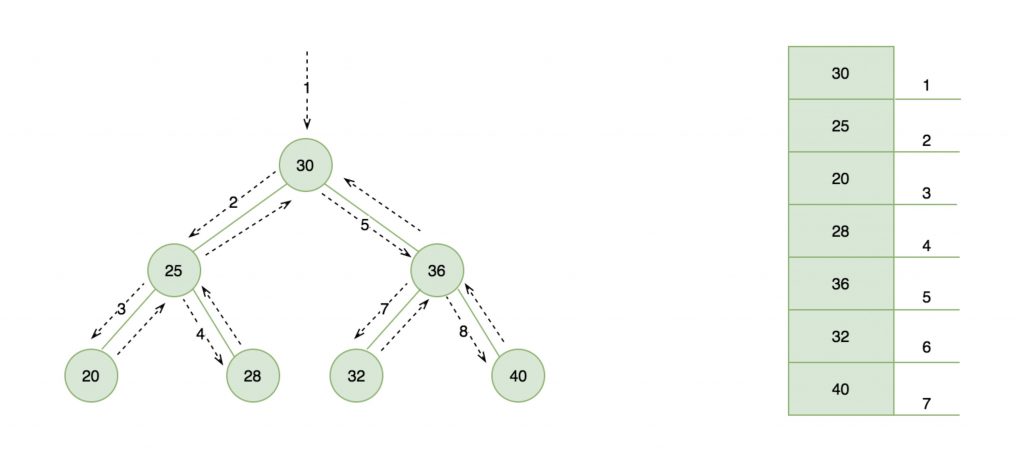
但是构造二叉排序树的目的,并不是为了排序,而是为了提高查找、插入和删除的速度。不管怎么说,在一个有序数据集上查找数据肯定比无序数据集要快,同时二叉排序树这种非线性结构,也非常有利于插入和删除的实现。
下面我们就来看看如何实现二叉排序树的插入、查找和删除以及它们对应的时间复杂度。
定义二叉排序树
首先,我们需要定义好表示二叉树节点的数据结构,还是通过二叉链表来存储二叉排序树,为了提高代码的复用性,我们将上篇教程定义的 Node 结构体抽取出来放到独立的 node.go 文件:
package main
import (
"fmt"
)
// Node 通过链表存储二叉树节点信息
type Node struct {
Data interface{}
Left *Node
Right *Node
}
func NewNode(data interface{}) *Node {
return &Node{
Data: data,
Left: nil,
Right: nil,
}
}
func (node *Node) GetData() string {
return fmt.Sprintf("%v", node.Data)
}
然后,我们新建一个 search.go 文件定义下二叉排序树对应的结构体,只需要根节点作为入口即可获取整棵树的结构:
package main
type BinarySearchTree struct {
root *Node
}
// NewBinarySearchTree 初始化二叉排序树
func NewBinarySearchTree(node *Node) *BinarySearchTree {
return &BinarySearchTree{
root: node,
}
}
这里我们通过结构体组合的方式声明二叉排序树的根节点是一个 Node 类型的指针,并为其定义了一个构造函数。
二叉排序树的插入
接下来,我们按照二叉排序树的定义,实现二叉排序树节点的插入方法:
// Insert 插入数据到二叉排序树
func (tree *BinarySearchTree) Insert(data interface{}) error {
var value int
var ok bool
if value, ok = data.(int); !ok {
return errors.New("暂时只支持int类型数据")
}
if node := tree.root; node == nil {
// 二叉排序树为空,则初始化
tree.root = NewNode(value)
return nil
} else {
// 否则找到要插入的位置插入新的节点
for node != nil {
if value < node.Data.(int) {
if node.Left == nil {
node.Left = NewNode(value)
break
}
node = node.Left
} else if value > node.Data.(int) {
if node.Right == nil {
node.Right = NewNode(value)
break
}
node = node.Right
} else {
return errors.New("对应数据已存在,请勿重复插入")
}
}
return nil
}
}
如果是空树,则将其作为根节点,否则判断插入节点数据与当前节点数据值的大小,如果小于当前节点数据值,则递归遍历左子树,找到对应的位置插入,如果大于当前节点数据值,则递归遍历右子树找到对应的位置插入。
我们可以写一段简单的测试代码测试节点插入方法:
func main() {
tree := NewBinarySearchTree(nil)
tree.Insert(3)
tree.Insert(2)
tree.Insert(5)
tree.Insert(1)
tree.Insert(4)
fmt.Println("中序遍历二叉排序树:")
midOrderTraverse(tree.root)
fmt.Println()
}
这里我们使用了上一篇编写的中序遍历方法 midOrderTraverse,对应的打印结果如下:

二叉排序树的查找
二叉排序树的删除比较复杂,我们先来看查找逻辑的实现,查找实现非常简单,和插入逻辑类似,依次递归比较就好了,直到目标节点数据值和待查找的数据值一致,则返回该节点的指针,或者返回空,表示没有找到:
// Find 查找值为data的节点
func (tree *BinarySearchTree) Find(data int) *Node {
if node := tree.root; node == nil {
// 二叉排序树为空返回空
return nil
} else {
// 否则返回值等于data的节点指针
for node != nil {
if data < node.Data.(int) {
node = node.Left
} else if data > node.Data.(int) {
node = node.Right
} else {
return node
}
}
return nil
}
}
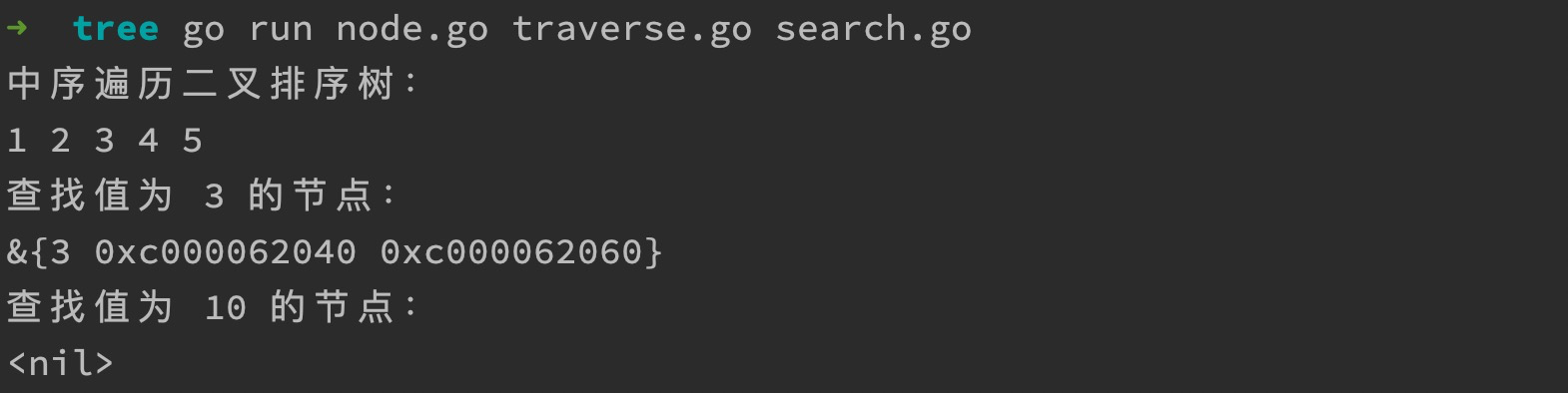
在上一步编写的测试代码基础上,我们可以通过编写如下代码打印找到节点的对象信息。
fmt.Println("查找值为 3 的节点:")
node := tree.Find(3)
fmt.Printf("%v\n", node)
fmt.Println("查找值为 10 的节点:")
node = tree.Find(10)
fmt.Printf("%v\n", node)
执行代码,打印结果如下:
二叉排序树的删除
二叉排序树的删除相对而言要复杂一些,需要分三种情况来处理:
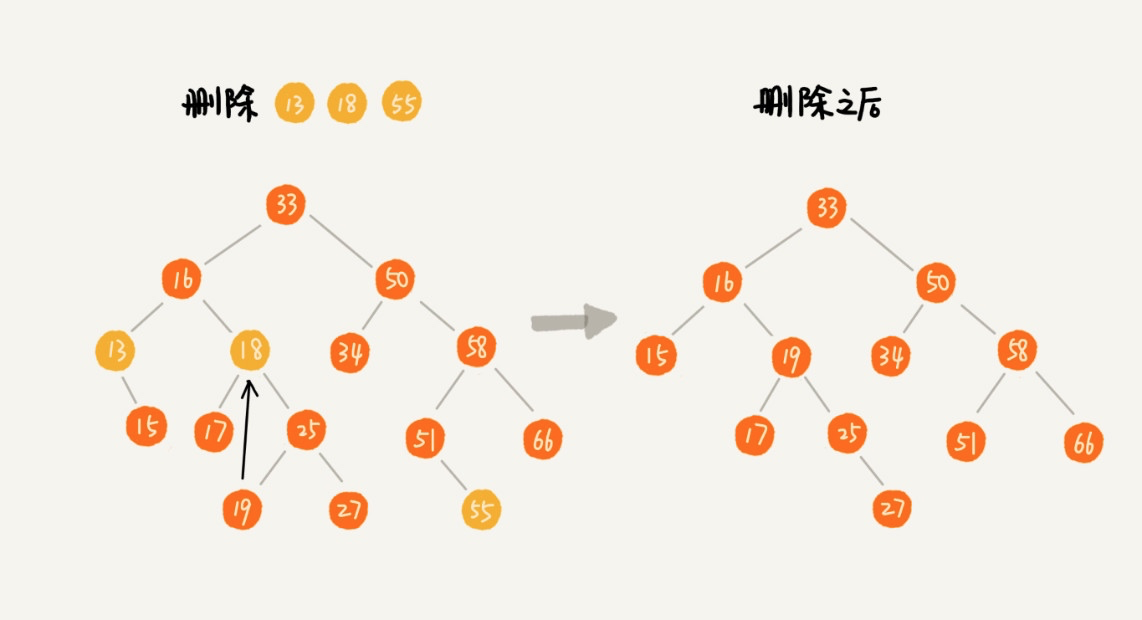
- 第一种情况:如果要删除的节点没有子节点,我们只需要直接将父节点中指向要删除节点的指针置为 nil。比如下图中的删除节点 55。
- 第二种情况:如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如下图中的删除节点 13。
- 第三种情况:如果要删除的节点有两个子节点,这就比较复杂了。我们需要先找到这个节点的右子树中节点值最小的节点,把它替换到要删除的节点上,然后再删除掉这个最小节点。因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如下图中的删除节点 18。(同理,也可以通过待删除节点的左子树中的最大节点思路来实现)
根据上面的思路,我们给出二叉排序树节点删除逻辑的实现代码:
// Delete 删除值为 data 的节点
func (tree *BinarySearchTree) Delete(data int) error {
if tree.root == nil {
return errors.New("二叉树为空")
}
p := tree.root
var pp *Node = nil // p 的父节点
// 找到待删除节点
for p != nil && p.Data.(int) != data {
pp = p
if p.Data.(int) < data {
// 当前节点值小于待删除值,去右子树查找
p = p.Right
} else {
// 否则去左子树查找
p = p.Left
}
}
if p == nil {
return errors.New("待删除节点不存在")
}
// 待删除节点有两个子节点,需要将待删除节点值设置为该节点右子树最小节点值,再删除右子树最小节点
if p.Left != nil && p.Right != nil {
minP := p.Right // 右子树中的最小节点
minPP := p // minP 的父节点
// 查找右子树中的最小节点
for minP.Left != nil {
minPP = minP
minP = minP.Left
}
p.Data = minP.Data // 将 minP 的数据设置到 p 中
p = minP // 下面就变成删除 minP 了
pp = minPP
}
// 应用待删除节点只有左/右子节点的逻辑
var child *Node
if p.Left != nil {
child = p.Left
} else if p.Right != nil {
child = p.Right
} else {
child = nil
}
if pp == nil {
// 删除跟节点
tree.root = nil
} else if pp.Left == p {
// 仅有左子节点
pp.Left = child
} else if pp.Right == p {
// 仅有右子节点
pp.Right = child
}
return nil
}
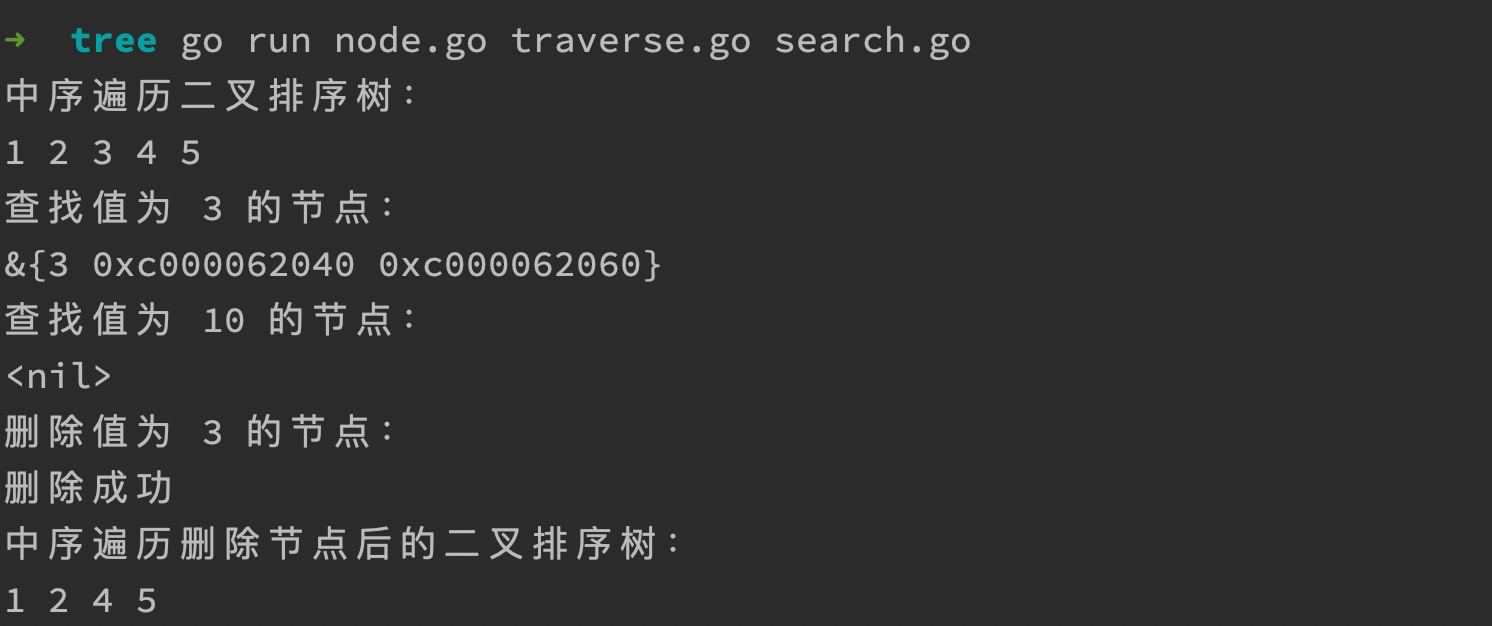
在之前测试代码的基础上,编写节点删除方法的测试代码:
fmt.Println("删除值为 3 的节点:")
err := tree.Delete(3)
if err != nil {
fmt.Printf("%v\n", err)
} else {
fmt.Println("删除成功")
}
fmt.Println("中序遍历删除节点后的二叉排序树:")
midOrderTraverse(tree.root)
fmt.Println()
执行 search.go,打印结果如下:
二叉排序树的时间复杂度
不论是插入、删除、还是查找,二叉排序树的时间复杂度都等于二叉树的高度,最好的情况当然是满二叉树或完全二叉树,此时根据完全二叉树的特性,时间复杂度是 O(logn),性能相当好,最差的情况是二叉排序树退化为线性表(斜树),此时的时间复杂度是 O(n),所以二叉排序树的形状也很重要,不同的形状会影响最终的操作性能,这也就引入了学院君接下来要继续深入介绍的二叉树内容 —— 平衡二叉树和红黑树。

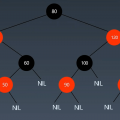



也就是说 第三种情况 把18的左子节点 17放到18那个位置 也是符合的 ?
是