哈希表
哈希表(HashTable,也叫散列表),是根据键名(Key)直接访问对应内存存储位置的数据结构。
其实现原理是通过哈希函数(也叫散列函数)将元素的键名映射为数组下标(转化后的值叫做哈希值或散列值),然后在对应下标位置存储记录值。当我们按照键名查询元素时,可以使用同样的哈希函数,将键名转化为数组下标,从对应的数组下标位置读取数据:
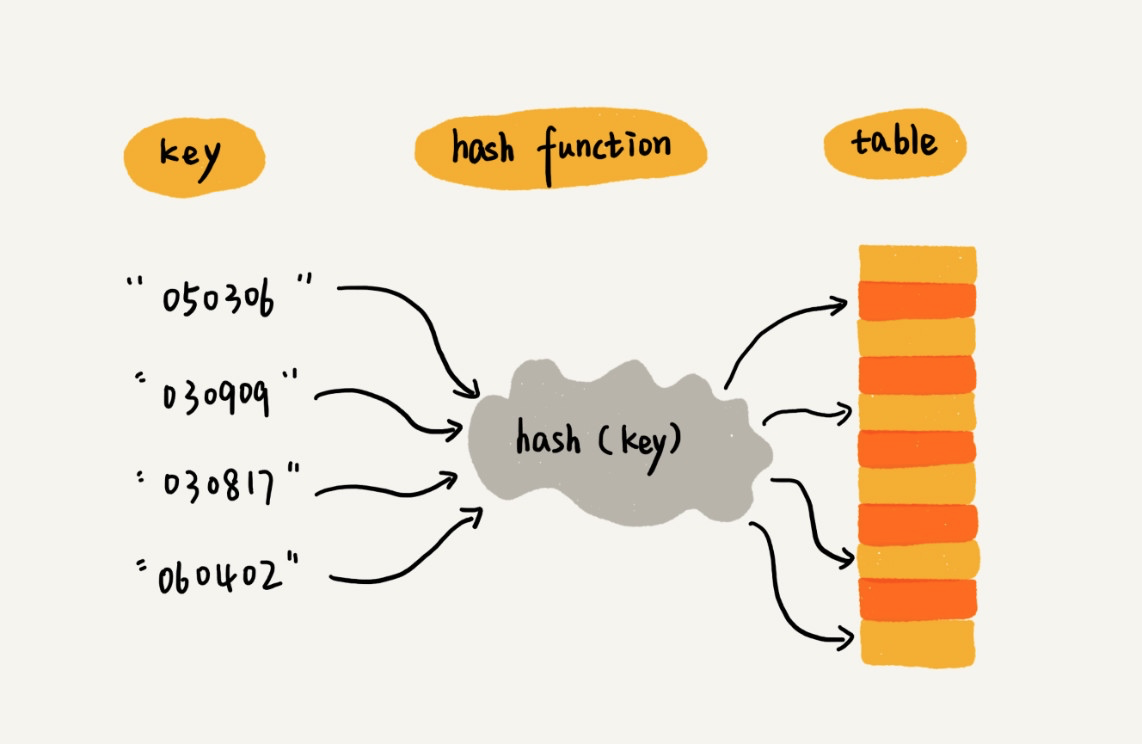
显然,哈希表使用了数组支持按照下标随机访问数据的特性,所以哈希表其实就是数组的一种扩展,由数组演化而来。可以说,没有数组,就没有哈希表。我们知道,数组访问元素的时间复杂度是 O(1),所以哈希表也是一样(不考虑哈希函数的复杂度的话),因此非常高效。
此外,我们也可以看到,哈希技术既是一种存储方法,也是一种查找方法。不过,与之前介绍的查找算法不同的是哈希表的不同记录之间不存在逻辑关系,因此最适合求解的问题是查找与给定值相等的记录,而不适合做范围查询。
哈希表中有两个关键的概念,一个是哈希函数(或者叫散列函数),一个是哈希冲突(或者叫散列冲突)。下面,我们来重点介绍这两个概念。
哈希函数与哈希冲突
哈希函数用于将键名经过处理后转化为对应的哈希值。具有以下特性:
- 哈希函数计算得到的哈希值是非负整数;
- 如果
key1 == key2,则hash(key1) == hash(key2); - 如果
key1 != key2,则hash(key1) != hash(key2)。
所谓哈希冲突,简单来说,指的是 key1 != key2 的情况下,通过哈希函数处理,hash(key1) == hash(key2),这个时候,我们就说发生了哈希冲突。
设计再好的哈希函数也无法避免哈希冲突,根本原因是哈希值是非负整数,总量是有限的,但是现实世界中要处理的键名是无限的,将无限的数据映射到有限的集合,肯定避免不了冲突。
事实上,如果不考虑哈希冲突,哈希表的查找效率是非常高的,时间复杂度是 O(1),比二分查找效率还要高,但是因为无法避免哈希冲突,所以哈希表查找的时间复杂度取决于哈希冲突,最坏的情况可能是 O(n),退化为顺序查找。这种情况在哈希函数设计不合理的情况下更糟。
哈希函数设计
要减少哈希冲突,提高哈希表操作效率,设计一个优秀的哈希函数至关重要,我们平时经常使用的 MD5 加密就是一个哈希函数,但是其实还有其他很多自定义的设计实现,要根据不同场景,设计不同的哈希函数来减少哈希冲突,而且哈希函数也要足够简单,否则执行哈希函数本身会成为哈希表的性能瓶颈。
我们日常很少会自己去设计哈希函数,但是做一些简单的了解还是有必要的。通常有以下几种哈希函数构造方法:
- 直接定址法:即
f(key) = a*key + b,f表示哈希函数,a、b是常量,key是键名; - 数字分析法:即对数字做左移、右移、反转等操作获取哈希值;
- 除数留余法:即
f(key) = key % p,p表示容器数量,这种方式通常用在将数据存放到指定容器中,如何决定哪个数据放到哪个容器,比如分表后插入数据如何处理(此时p表示拆分后数据表的数量),分布式 Redis 如何存放数据(此时p表示几台 Redis 服务器); - 随机数法:即
f(key) = random(key),比如负载均衡的 random 机制。
以上只是一些比较常见的哈希函数设计思路,还有很多其他的设计方法,这里就不一一列举了。
哈希冲突处理
我们前面说过,设计再好的哈希函数也不能完全避免哈希冲突,我们只能优化自己的实现让哈希冲突尽可能少出现罢了,如果出现了哈希冲突,该如何处理呢?下面给出一些思路:
- 开放寻址法:该方法又可以细分为三种 —— 线性寻址、二次探测、随机探测。线性寻址表示出现哈希冲突之后,就去寻找下一个空的哈希地址;线性寻址步长是 1,二次探测步长是线性寻址步长的 2 次方,其它逻辑一样;同理,随机探测每次步长随机。不管哪种探测方法,哈希表中空闲位置不多的时候,哈希冲突的概率就会提高,为了保证操作效率,我们会尽可能保证哈希表中有一定比例的空闲槽位,我们用装载因子来表示空位的多少,装载因子=填入元素/哈希表长度,装载因子越大,表明空闲位置越少,冲突越多,哈希表性能降低。
- 再哈希函数法:发生哈希冲突后,换一个哈希函数计算哈希值
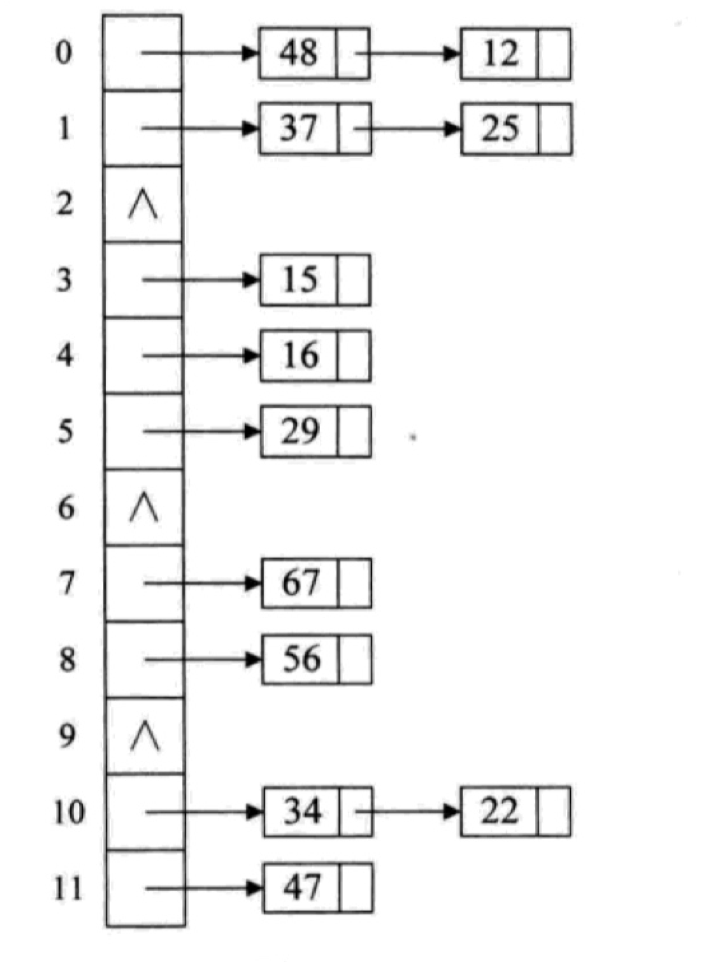
- 链地址法:发生哈希冲突后,将对应数据链接到该哈希值映射的上一个值之后,即将哈希值相同的元素放到相同槽位对应的链表中。链地址法即使在哈希冲突很多的情况下,也可以保证将所有数据存储到哈希表中,但是也引入了遍历单链表带来性能损耗。
介绍完以上内容之后,想必你对如何打造工业级哈希表已经心中有数。主要考虑因素包含以下几个方面:
- 哈希函数设置合理,不能太过复杂,成为性能瓶颈;
- 设置装载因子阈值,支持动态扩容,装载因子阈值设置要充分权衡时间、空间复杂度;
- 如果一次性扩容耗时长,可采取分批扩容的策略,达到阈值后只申请空间,不搬移数据,以后每插入一条数据,搬移一个旧数据,最后逐步完成搬移,期间为了兼容新老哈希表查询,可以先查新表,再查老表;
- 哈希冲突解决办法:开放寻址法在数据量较小、装载因子小的时候(小于1)选用;链表法可以容忍装载因子大于1,适合存储大对象、大数据量的哈希表,且更加灵活,支持更多优化策略。
补充一张链地址法处理哈希冲突的图示:
哈希算法
我们前面分享了哈希表、哈希函数和哈希冲突,哈希算法简单理解就是实现前面提到的哈希函数的算法,用于将任意长度的二进制值串映射为固定长度的二进制值串,映射之后得到的二进制值就是哈希值。
我们日常开发中最常见的哈希算法应用就是通过 MD5 对数据进行加密了:
package main
import (
"crypto/md5"
"fmt"
)
func main() {
data := []byte("Hello, World!")
hash := md5.Sum(data)
fmt.Printf("原始值: %s\n", data)
fmt.Printf("MD5值: %x\n", hash)
}
这里的 md5.Sum 就是一个哈希函数。执行上述代码,打印结果如下:

哈希算法的一般特性如下:
- 从哈希值不能反向推导出原始数据(所以哈希算法也叫单向算法,不可逆);
- 对输入数据非常敏感,哪怕原始数据只修改了一个比特,最后得到的哈希值也大不相同;
- 哈希冲突的概率要很小,对于不同的原始数据,哈希值相同的概率非常小;
- 哈希算法的执行效率要尽量高效,针对较长的文本,也能快速地计算出哈希值。
哈希算法的应用
1、场景一:安全加密
我们日常用户密码加密通常使用的都是 md5、sha 等哈希函数,因为不可逆,而且微小的区别加密之后的结果差距很大,所以安全性更好。
2、场景二:唯一标识
比如我们的 URL 字段或者图片字段要求不能重复,这个时候就可以通过对相应字段值做 md5 处理,将数据统一为 32 位长度从数据库索引构建和查询角度效果更好,此外,还可以对文件之类的二进制数据做 md5 处理,作为唯一标识,这样判定重复文件的时候更快捷。
3、场景三:数据校验
比如我们从网上下载的很多文件(尤其是 P2P 站点资源),都会包含一个 MD5 值,用于校验下载数据的完整性,避免数据在中途被劫持篡改。
4、场景五:哈希函数
前面我们已经提到,PHP 中的 md5、sha1、hash 等函数都是基于哈希算法计算哈希值。
5、场景五:负载均衡
对于同一个客户端上的请求,尤其是已登录用户的请求,我们需要将其会话请求都路由到同一台机器,以保证数据的一致性,这可以借助哈希算法来实现,通过用户 ID 尾号对总机器数取模(取多少位可以根据机器数定),将结果值作为机器编号。
6、场景六:分布式缓存
分布式缓存和其他机器或数据库的分布式不一样,因为每台机器存放的缓存数据不一致,每当缓存机器扩容时,需要对缓存存放机器进行重新索引(或者部分重新索引),这里应用到的也是哈希算法的思想。后面我们介绍 Redis 系列的时候会系统阐述这一块。