Go 数据结构和算法篇（十六）：二叉树的遍历

二叉树的遍历指的是从根节点出发，按照某种次序依次访问二叉树中的所有节点，使得每个节点被访问一次且仅被访问一次。

有多种方式可以遍历二叉树，如果按照从左到右的习惯方式，主要分为三种：前序遍历、中序遍历和后序遍历。下面我们简单介绍这几种遍历方式及对应实现算法，所谓的前序、中序和后序都是以根节点作为参照系。

前序遍历

从根节点开始，先遍历左子树，再遍历右子树（对于子树的子树，依此类推），如果二叉树为空，则返回空：

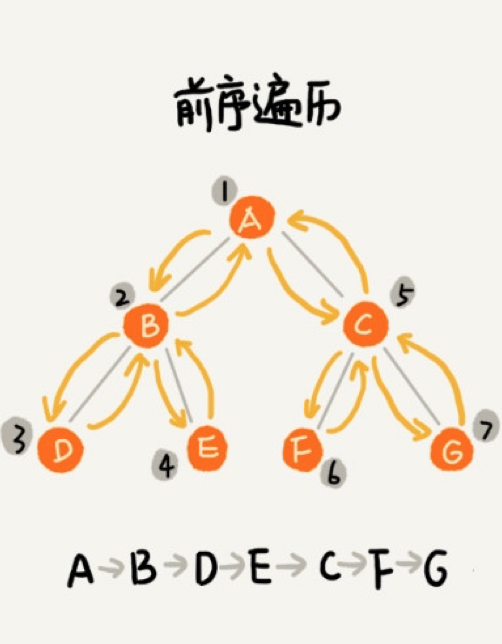
显然，我们可以通过递归来实现二叉树的前序遍历逻辑，对应的 Go 实现代码如下：

package main
​
import (
  "fmt"
)
​
// Node 通过链表存储二叉树节点信息
type Node struct {
  Data  interface{}
  Left  *Node
  Right *Node
}
​
func NewNode(data interface{}) *Node {
  return &Node{
    Data:  data,
    Left:  nil,
    Right: nil,
  }
}
​
func (node *Node) GetData() string {
  return fmt.Sprintf("%v", node.Data)
}
​
// 前序遍历
func preOrderTraverse(treeNode *Node) {
  // 节点为空则退出当前递归
  if treeNode == nil {
    return
  }
  // 否则先打印当前节点值
  fmt.Printf("%s ", treeNode.GetData())
  // 然后对左子树和右子树做前序遍历
  preOrderTraverse(treeNode.Left)
  preOrderTraverse(treeNode.Right)
}
​
// 测试代码
func main() {
  // 初始化一个简单的二叉树
  node1 := NewNode(0) // 根节点
  node2 := NewNode("1")
  node3 := NewNode(2.0)
  node1.Left = node2
  node1.Right = node3
​
  // 前序遍历这个二叉树
  fmt.Print("前序遍历: ")
  preOrderTraverse(node1)
  fmt.Println()
}

这里，我们使用了链表结构来存储二叉树，并且通过 interface{} 空接口类型声明二叉树节点支持存储任意类型数据。

执行上述代码，打印结果如下：

中序遍历

中序遍历会从左子树最左侧的节点开始，然后从左到右依次遍历左子树，根节点，最后是右子树（依然是从最左侧节点开始从左到右的顺序遍历），如果二叉树为空，则返回空：

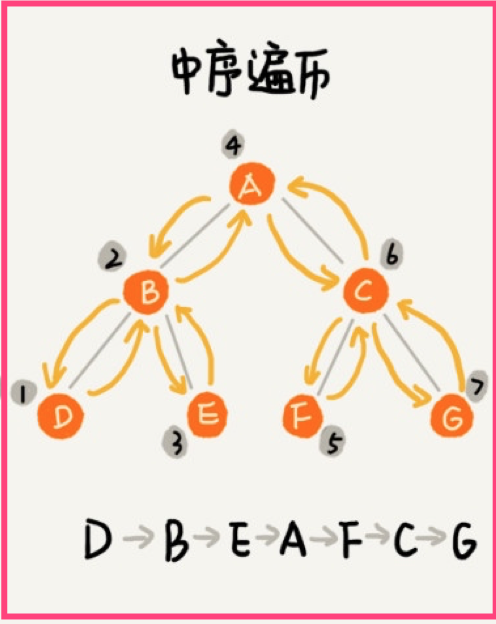
我们在上面的示例代码中添加中序遍历实现代码：

package main

import (
  "fmt"
)
​
...
​
// 中序遍历
func midOrderTraverse(treeNode *Node) {
  // 节点为空则退出当前递归
  if treeNode == nil {
    return
  }
  // 否则先从左子树最左侧节点开始遍历
  midOrderTraverse(treeNode.Left)
  // 打印位于中间的根节点
  fmt.Printf("%s ", treeNode.GetData())
  // 最后按照和左子树一样的逻辑遍历右子树
  midOrderTraverse(treeNode.Right)
}
​
func main() {
  ...
​
  // 中序遍历这个二叉树
  fmt.Print("中序遍历: ")
  midOrderTraverse(node1)
  fmt.Println()
}
​

执行上述代码，打印结果如下：

后序遍历

最后来看后序遍历，后序遍历也是从左子树最左侧的节点开始，不过会从左到右先遍历完叶子节点，再遍历父节点，遍历完左子树后，直接从右子树最左侧节点开始，按照和左子树同样的顺序遍历完右子树，最后访问根节点：

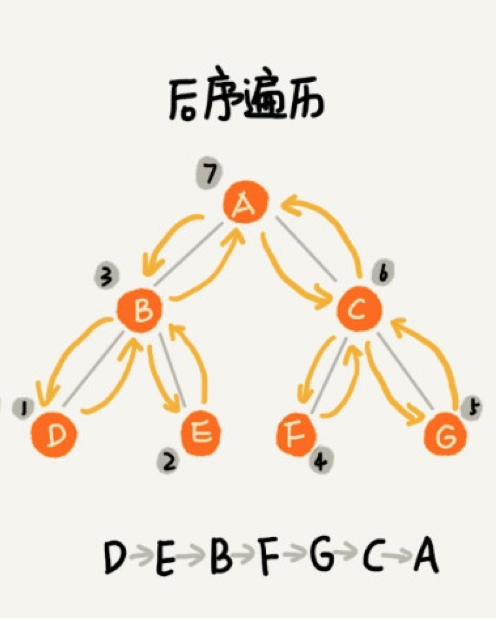
有了前面的基础，编写后序遍历实现代码就相当轻松了：

package main
​
import (
  "fmt"
)
​
...
​
// 后序遍历
func postOrderTraverse(treeNode *Node) {
  // 节点为空则退出当前递归
  if treeNode == nil {
    return
  }
  // 否则先遍历左子树
  postOrderTraverse(treeNode.Left)
  // 再遍历右子树
  postOrderTraverse(treeNode.Right)
  // 最后访问根节点
  fmt.Printf("%s ", treeNode.GetData())
}
​
func main() {
  ...
​
  // 后序遍历这个二叉树
  fmt.Print("后序遍历: ")
  postOrderTraverse(node1)
  fmt.Println()
}

执行上述代码，打印结果如下：

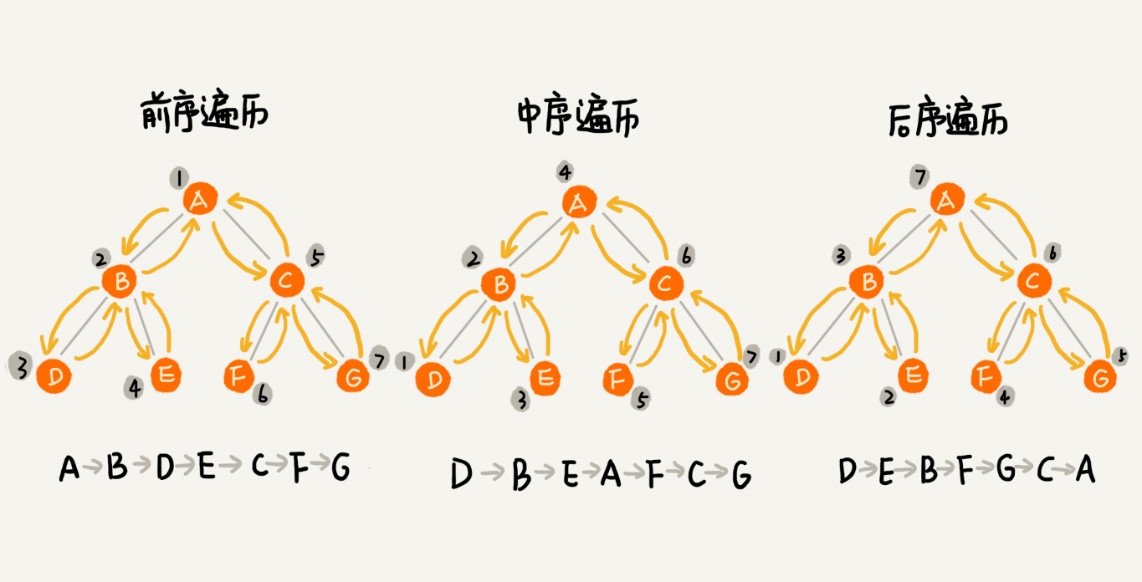
可以看到，不同的遍历方式从不同维度将二叉树这种非线性的结构变成了某种意义上的线性序列，从而方便计算机操作。

感兴趣的同学还可以通过并发模式来编排二叉树的上述遍历行为。