Go 数据结构和算法篇（一）：链表

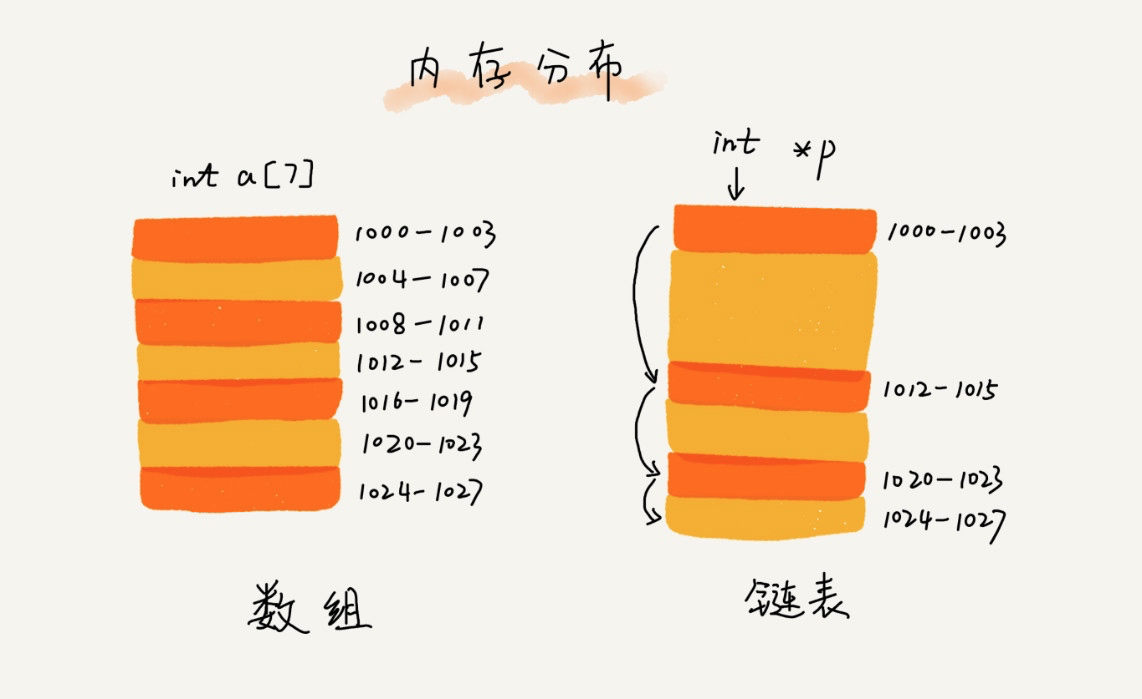
链表是一种数据结构，和数组不同，链表并不需要一块连续的内存空间，它通过「指针」将一组零散的内存块串联起来使用，如图所示：

单链表

链表有多种类型，最简单的是单链表，单链表是最原生的链表，其结构如图所示：

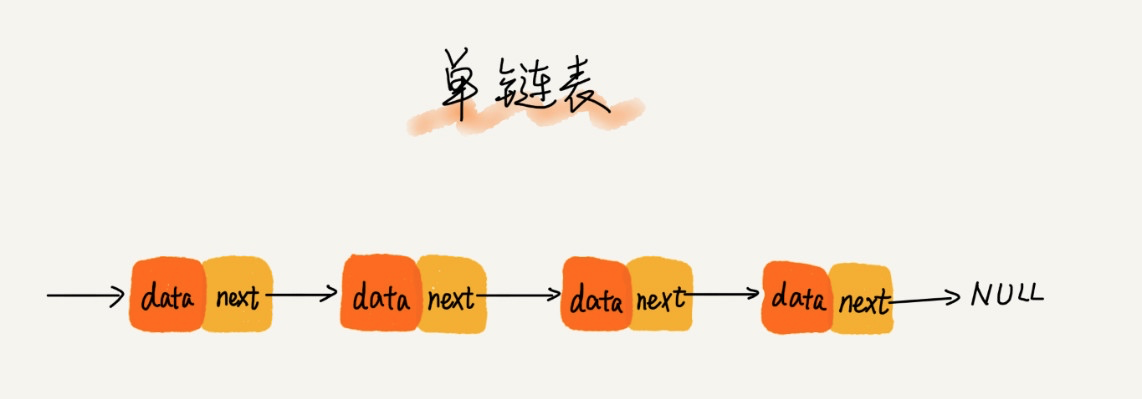
单链表中有两个节点比较特殊，分别是第一个节点和最后一个节点。我们通常把第一个节点叫作头节点，把最后一个结点叫作尾节点。

其中，头节点用来记录链表的基地址，有了它，我们就可以遍历得到整条链表。而尾节点特殊的地方是：指针不是指向下一个结点，而是指向一个空地址 NULL，表示这是链表上最后一个节点。

对于其他普通节点而言，每个节点至少使用两个内存空间：一个用于存储实际数据，另一个用于存储下一个元素的指针，从而形成出一个节点序列，构建链表。

对单链表而言，理论上来说，插入和删除节点的时间复杂度是 O(1)，查询节点的时间复杂度是 O(n)。

基于 Go 语言实现单链表

下面我们基于 Go 语言来实现简单的单链表，并实现添加节点、遍历链表、查找节点和获取链表长度等功能：

package main

import (
    "fmt"
)

// 定义节点
type Node struct {
    Value int
    Next  *Node
}

// 初始化头节点
var head = new(Node)

// 添加节点
func addNode(t *Node, v int) int {
    if head == nil {
        t = &Node{v, nil}
        head = t
        return 0
    }

    if v == t.Value {
        fmt.Println("节点已存在:", v)
        return -1
    }

   // 如果当前节点下一个节点为空
    if t.Next == nil {
        t.Next = &Node{v, nil}
        return -2
    }

   // 如果当前节点下一个节点不为空
    return addNode(t.Next, v)
}

// 遍历链表
func traverse(t *Node) {
    if t == nil {
        fmt.Println("-> 空链表!")
        return
    }

    for t != nil {
        fmt.Printf("%d -> ", t.Value)
        t = t.Next
    }

    fmt.Println()
}

// 查找节点
func lookupNode(t *Node, v int) bool {
    if head == nil {
        t = &Node{v, nil}
        head = t
        return false
    }

    if v == t.Value {
        return true
    }

    if t.Next == nil {
        return false
    }

    return lookupNode(t.Next, v)
}

// 获取链表长度
func size(t *Node) int {
    if t == nil {
        fmt.Println("-> 空链表!")
        return 0
    }

    i := 0
    for t != nil {
        i++
        t = t.Next
    }

    return i
}

// 入口函数
func main() {
    fmt.Println(head)
    head = nil
    // 遍历链表
    traverse(head) 
    // 添加节点 
    addNode(head, 1)
    addNode(head, -1)
    // 再次遍历
    traverse(head)
    // 添加更多节点
    addNode(head, 10)
    addNode(head, 5)
    addNode(head, 45)
    // 添加已存在节点
    addNode(head, 5)
    // 再次遍历
    traverse(head)

   // 查找已存在节点
    if lookupNode(head, 5) {
        fmt.Println("该节点已存在!")
    } else {
        fmt.Println("该节点不存在!")
    }

   // 查找不存在节点 
    if lookupNode(head, -100) {
        fmt.Println("该节点已存在!")
    } else {
        fmt.Println("该节点不存在!")
    }
}

执行上述代码，打印结果如下：

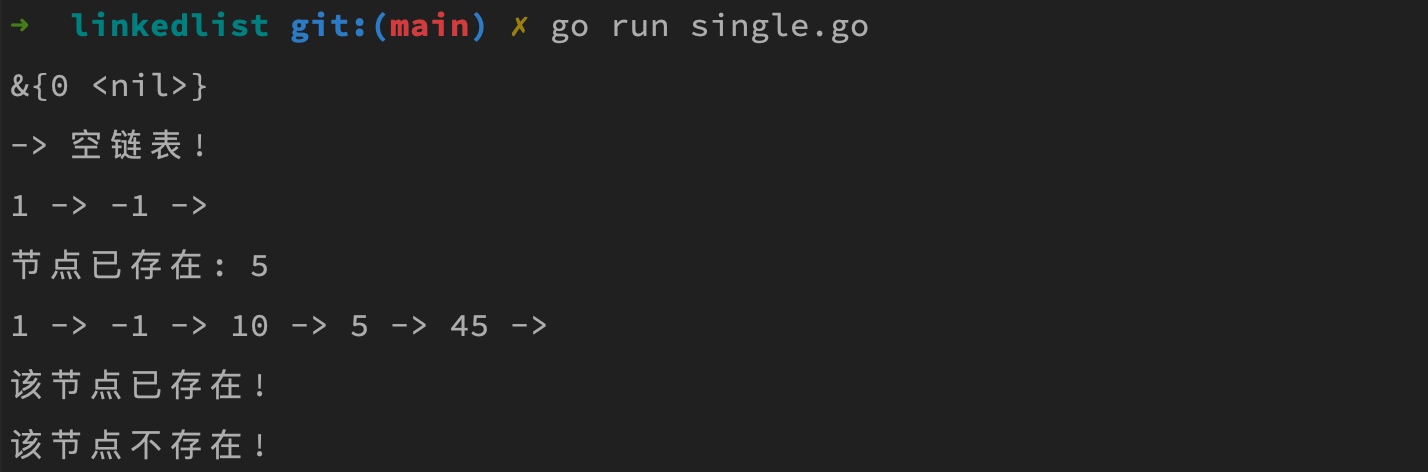
循环链表

还可以在单链表的基础上扩展出循环链表，循环链表和单链表的区别是尾节点指向了头节点，从而首尾相连，有点像贪吃蛇，可用于解决「约瑟夫环」问题，循环链表的结构如图所示：

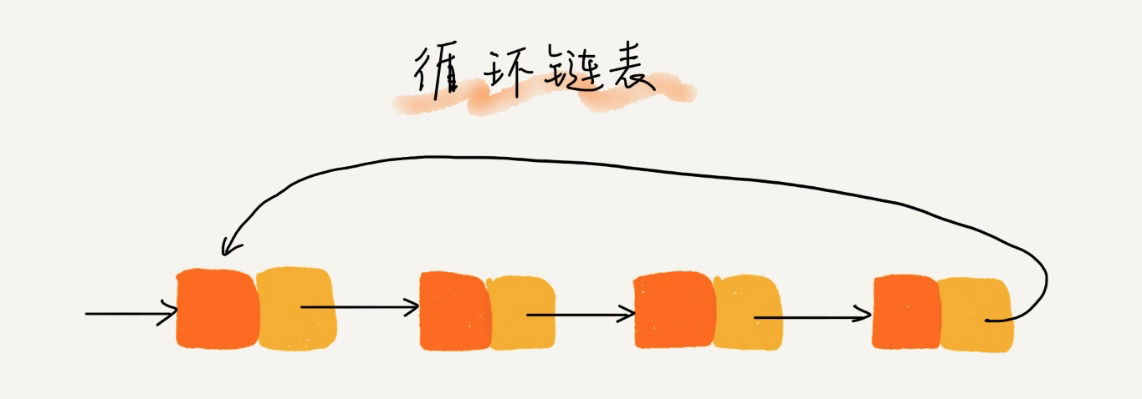
感兴趣的同学可以参考单链表自行通过 Go 语言实现循环链表，非常简单，就是将尾节点的后驱节点指针执行头节点即可。

双向链表

比较常见的链表结构还有双向链表，顾名思义，与单链表的区别是双向链表除了有一个指向下一个节点的指针外，还有一个用于指向上一个节点的指针，从而实现通过 O(1) 复杂度找到上一个节点。正是因为这个指针，使得双向链表在插入、删除节点时比单链表更高效。

虽然我们前面已经提到单链表插入、删除时间复杂度已经是 O(1) 了，但是这只是针对插入、删除操作本身而言，以删除为例，删除某个节点后，需要将其前驱节点的指针指向被删除节点的下一个节点：

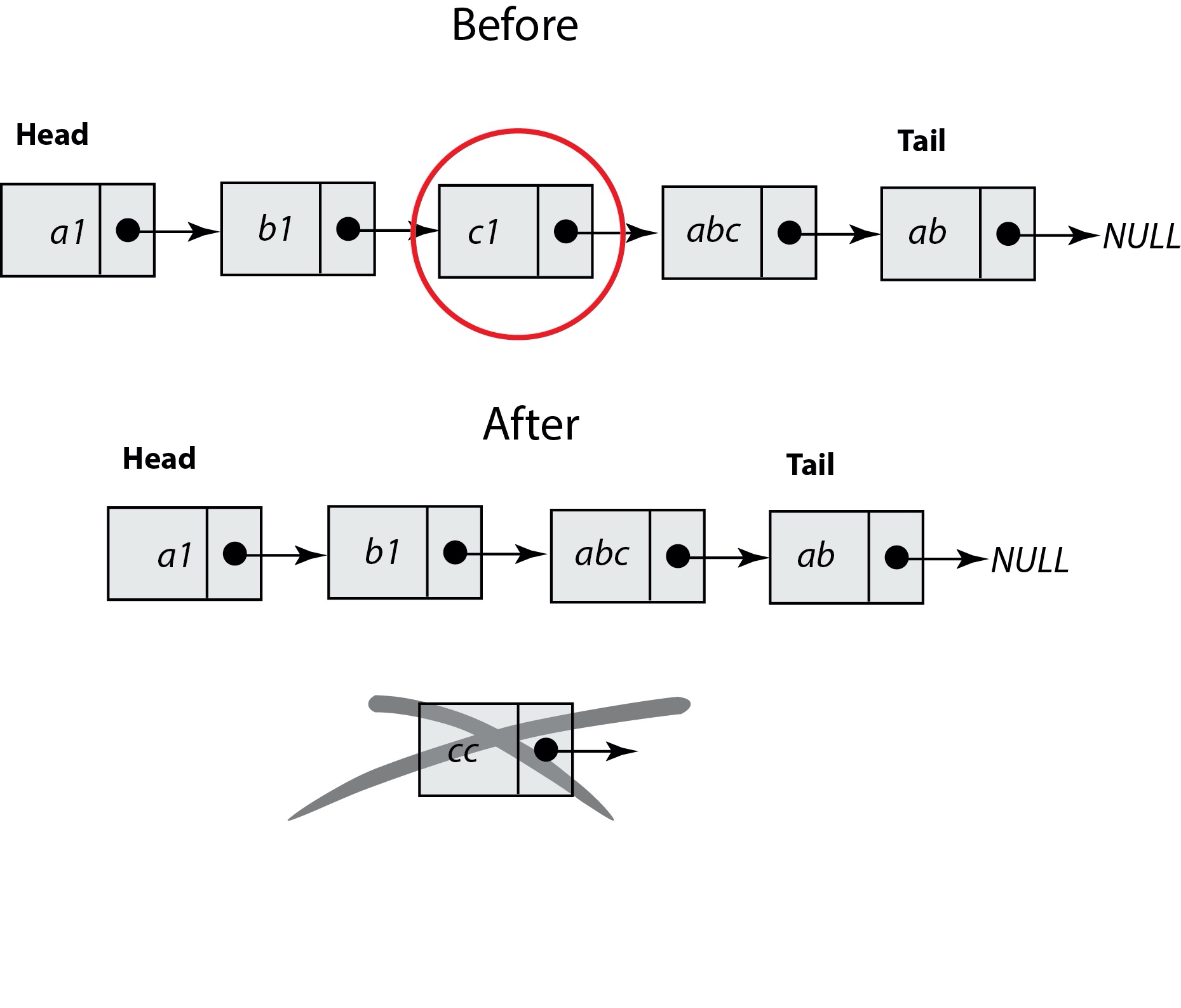
这样，我们还需要获取其前驱节点，在单链表中获取前驱节点的时间复杂度是 O(n)，所以综合来看单链表的删除、插入操作时间复杂度也是 O(n)，而双向链表则不然，它有一个指针指向上一个节点，所以其插入和删除时间复杂度才是真正的 O(1)：

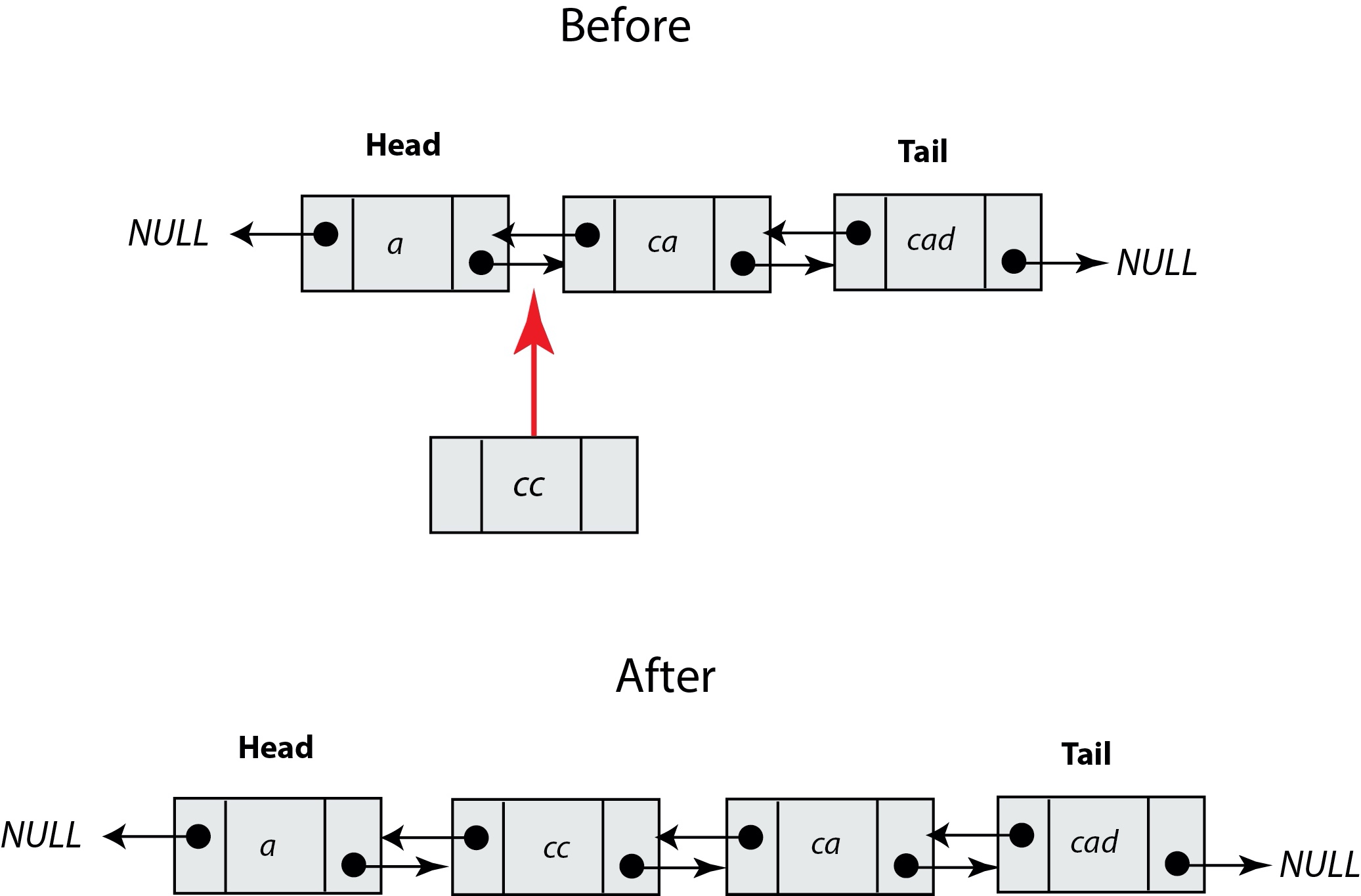
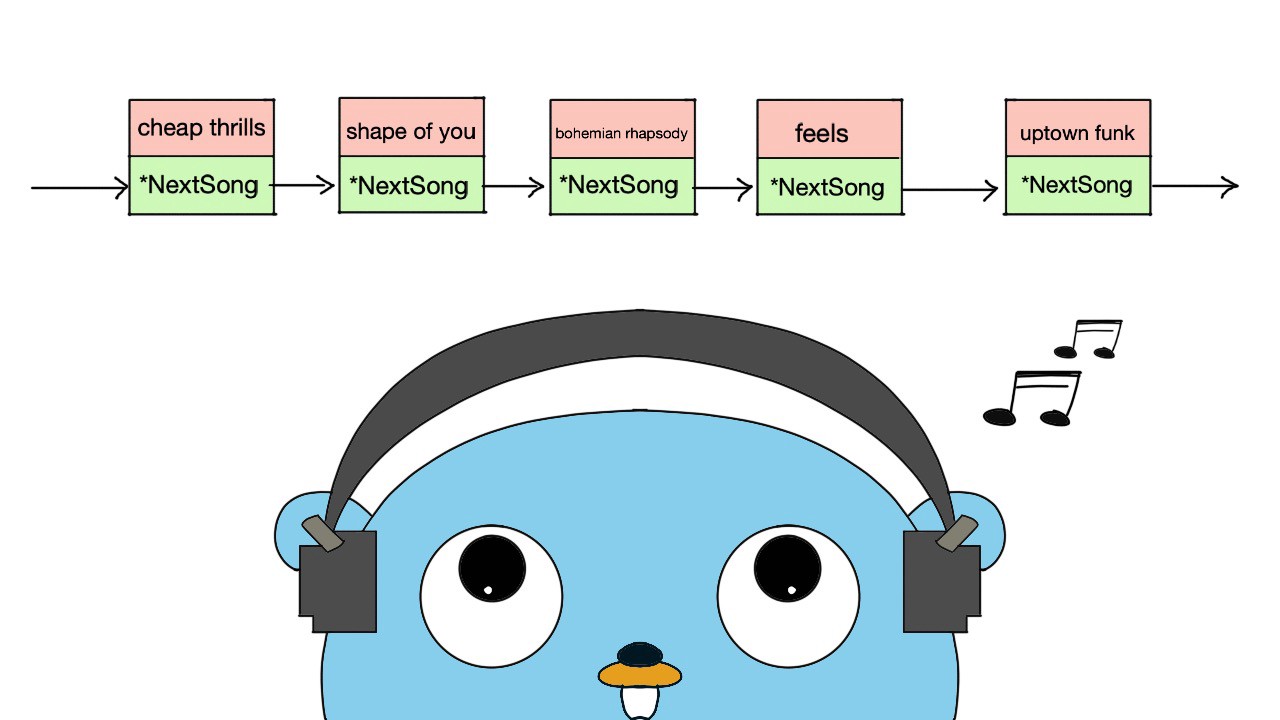
此外，对于有序链表而言，双向链表的查询效率显然也要高于单链表，不过更优的时间复杂度是靠更差的空间复杂度换取的，双向链表始终需要单链表的两倍空间，不过正如我们之前说的，在 Web 应用中，时间效率优先级更高，所以我们通常都是空间换时间来提高性能，Java 的 LinkedHashMap 底层就用到了双向链表，此外在日常应用中，音乐软件的播放列表也是一个典型的双向链表（支持在上一首和下一首之间进行切换）。

双向链表的结构如图所示：

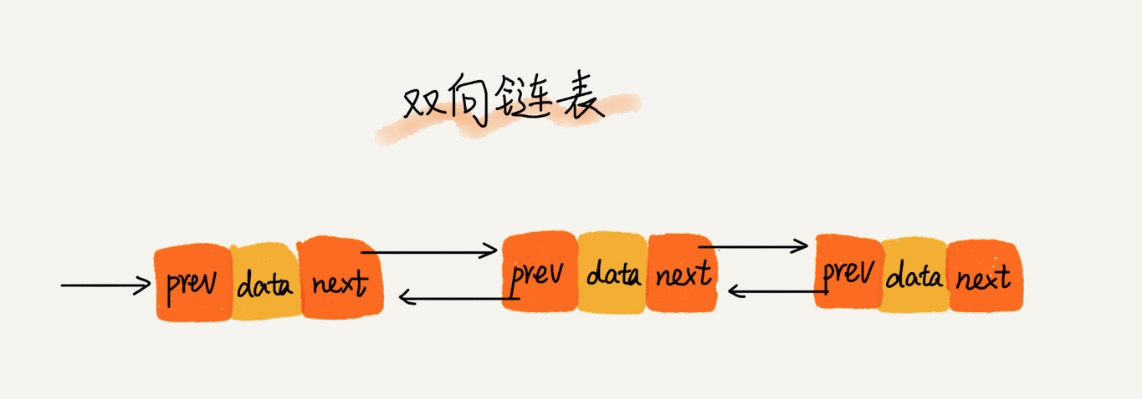
基于 Go 语言实现双向链表

下面我们来看看如何基于 Go 语言实现双向链表，和单链表相比，双向链表需要多维护一个前驱节点指针，以及支持反向遍历：

package main

import (
    "fmt"
)

// 定义节点
type Node struct {
    Value    int
    Previous *Node
    Next     *Node
}

// 添加节点
func addNode(t *Node, v int) int {
    if head == nil {
        t = &Node{v, nil, nil}
        head = t
        return 0
    }

    if v == t.Value {
        fmt.Println("节点已存在:", v)
        return -1
    }

    // 如果当前节点下一个节点为空
    if t.Next == nil {
        // 与单链表不同的是每个节点还要维护前驱节点指针
        temp := t
        t.Next = &Node{v, temp, nil}
        return -2
    }

    // 如果当前节点下一个节点不为空
    return addNode(t.Next, v)
}

// 遍历链表
func traverse(t *Node) {
    if t == nil {
        fmt.Println("-> 空链表!")
        return
    }

    for t != nil {
        fmt.Printf("%d -> ", t.Value)
        t = t.Next
    }

    fmt.Println()
}

// 反向遍历链表
func reverse(t *Node) {
    if t == nil {
        fmt.Println("-> 空链表!")
        return
    }

    temp := t
    for t != nil {
        temp = t
        t = t.Next
    }

    for temp.Previous != nil {
        fmt.Printf("%d -> ", temp.Value)
        temp = temp.Previous
    }

    fmt.Printf("%d -> ", temp.Value)
    fmt.Println()
}

// 获取链表长度
func size(t *Node) int {
    if t == nil {
        fmt.Println("-> 空链表!")
        return 0
    }

    n := 0
    for t != nil {
        n++
        t = t.Next
    }

    return n
}

// 查找节点
func lookupNode(t *Node, v int) bool {
    if head == nil {
        return false
    }

    if v == t.Value {
        return true
    }

    if t.Next == nil {
        return false
    }

    return lookupNode(t.Next, v)
}

// 初始化头节点
var head = new(Node)

func main() {
    fmt.Println(head)
    head = nil
    // 遍历链表
    traverse(head)
    // 新增节点
    addNode(head, 1)
    // 再次遍历
    traverse(head)
    // 继续添加节点
    addNode(head, 10)
    addNode(head, 5)
    addNode(head, 100)
    // 再次遍历
    traverse(head)
    // 添加已存在节点
    addNode(head, 100)
    fmt.Println("链表长度:", size(head))
    // 再次遍历
    traverse(head)
    // 反向遍历
    reverse(head)

    // 查找已存在节点
    if lookupNode(head, 5) {
        fmt.Println("该节点已存在!")
    } else {
        fmt.Println("该节点不存在!")
    }
}

运行上述代码，打印结果如下：

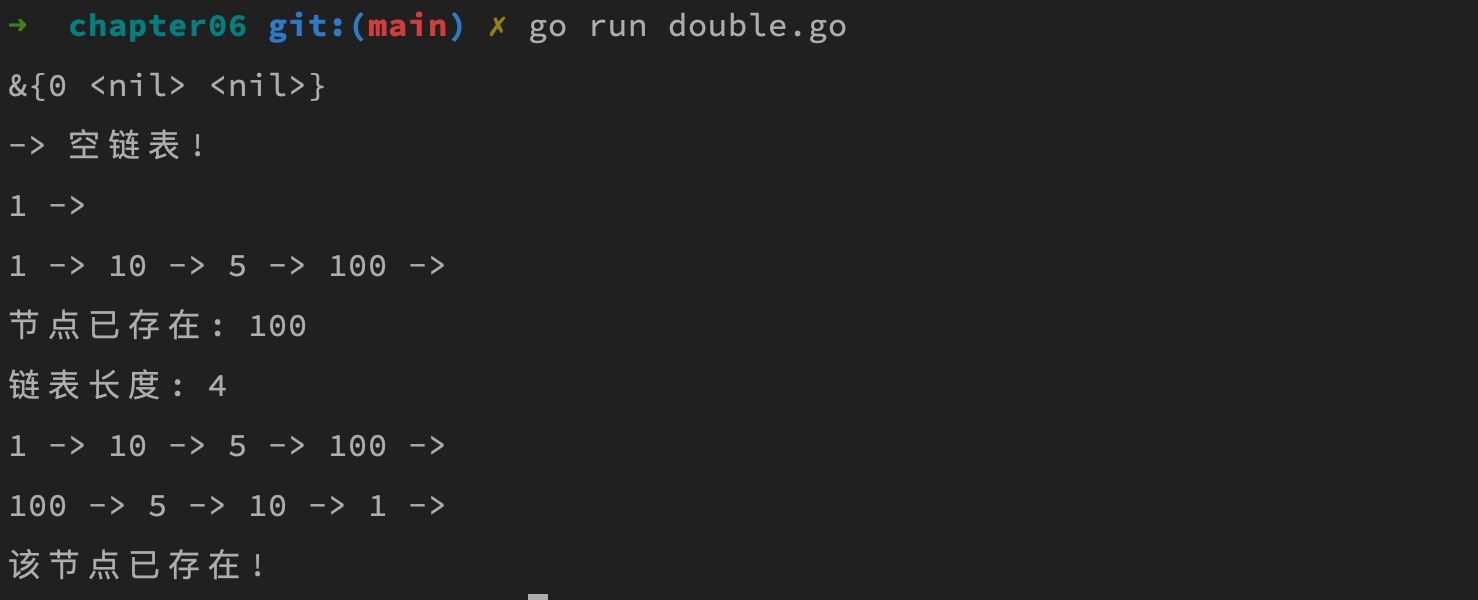
双向循环链表

最后，我们要介绍的是结合循环链表和双向链表为一体的双向循环链表：

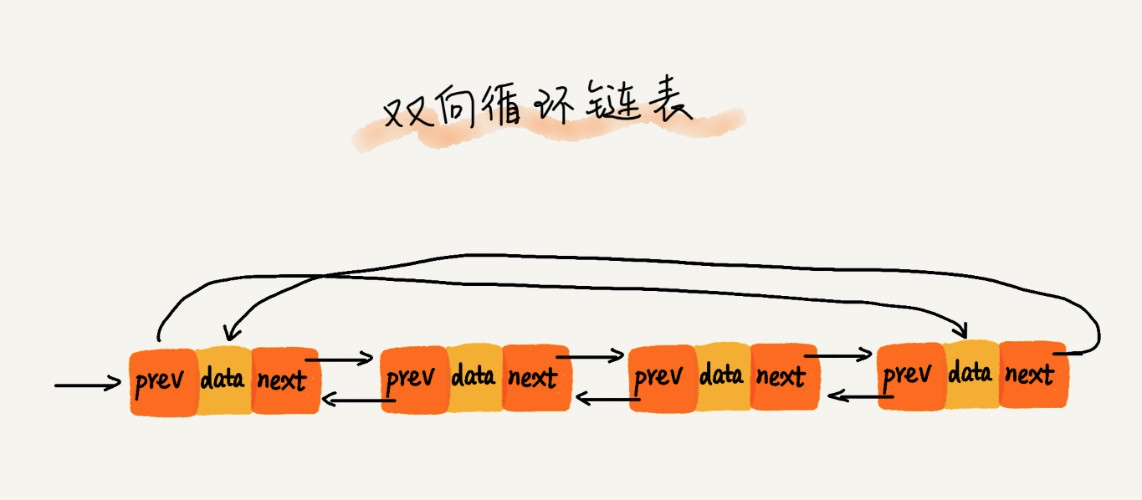
感兴趣的同学可以参考双向链表自行基于 Go 语言实现双向循环链表，其实就是将双向链表的首尾通过指针连接起来，对于支持循环播放的音乐列表其实就是个双向循环链表结构。