题目
今天来看一个考察程序员基本功的数组面试题,看起来仍然很简单,不过通过这个题目的不同解法,可以快速检验你是初级程序员还是资深程序员,一起来看下吧:
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
解法一
对于新人而言,可以很快写出下面这样的实现代码:
func reOrderArrayV1(arr []int) []int {
var oddArr, evenArr []int
for _, value := range arr {
if value % 2 == 0 {
evenArr = append(evenArr, value)
} else {
oddArr = append(oddArr, value)
}
}
return append(oddArr, evenArr...)
}
非常简单,先声明两个数组切片,分别用于存储奇数和偶数,然后遍历待排序的数组切片,根据是否可以被 2 整除将切片数据分发到偶数和奇数切片,最后将偶数切片数据追加到奇数切片之后作为新的切片返回。
为上面这段代码编写测试代码:
func main() {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
fmt.Println("排序前:", arr)
fmt.Println("排序后:", reOrderArrayV1(arr))
}
执行之后打印结果如下,说明代码可以正常工作:

解法二
上面的实现虽然简单易懂,不过扩展性很差,比如现在是按照奇偶数排序,如果换一下排序条件,变成按照是否可以被3整除,或者按照正负数进行排序,则需要重写整个排序方法实现代码。
实现相同功能的代码,在满足最基本的正确性的基础上,新人和老鸟的区别往往就是体现在扩展性、鲁棒性、高性能这些更高层级的代码艺术上。
下面我们从扩展性的角度出发,将排序条件抽取出来作为可定制的闭包参数从外部传入排序函数:
// 根据指定闭包对数组切片排序
func reOrderArrayV2(arr []int, orderFunc func(int) bool) []int {
// 小于等于1个元素无需处理
if arr == nil || len(arr) <= 1 {
return arr
}
// 设置两个指针,从头尾往中间移动
i := 0
j := len(arr) - 1
// 头指针不能越过尾指针,否则退出
// 以奇偶数排序为例,i 从左到右寻找偶数,j 从右到左寻找奇数
// 该循环执行完毕后,i 左侧的都是奇数,j 右侧的都是偶数,也就完成了顺序调整
for i < j {
// 如果不符合条件,则头指针后移,否则中断
// 以 orderFunc 为偶数判断函数为例,返回 false 表示是奇数
// 题目要求奇数排在前面,因此,当 i 对应值是奇数时,往后移一位,然后继续下一个循环,直到 i==j 或者遇到第一个偶数中断
for i < j && !orderFunc(arr[i]) {
i++
}
// 如果符合条件,则尾指针前移,否则中断
// 还是以 orderFunc 为偶数判断函数为例,返回 true 表示是偶数
// 题目要求偶数排在后面,因此,当 j 对应值是偶数时,往前移一位,然后继续下一个循环,直到 j==i 或者遇到第一个奇数中断
for i < j && orderFunc(arr[j]) {
j--
}
// 如果 i < j,则交换对应值的位置
// 以奇偶数为例,此时 arr[i] 是偶数,arr[j] 是奇数,则交换两个值,将奇数放到前面,偶数放到后面
if i < j {
arr[i], arr[j] = arr[j], arr[i]
}
// 继续下一个循环,直到 i==j,此时 i 左侧都是奇数,j 右侧都是偶数,所有奇数都排到了偶数前面
}
return arr
}
// 排序条件:是否是偶数
func isEven(num int) bool {
return num & 1 == 0
}
这样一来,reOrderArrayV2 函数就与具体的排序条件解耦了,我们可以通过外部参数传入任意的排序条件:
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
fmt.Println("排序前:", arr)
fmt.Println("排序后:", reOrderArrayV2(arr, isEven))
打印结果如下,表明排序成功:

下次你想通过正负数、是否可以被3整除之类的排序条件做排序,只需要编写对应的排序条件判定函数,然后传入 reOrderArrayV2排序函数即可,排序函数本身无需做任何调整:
// 是否是整数(为 true 的值放在后面)
func isPositive(num int) bool {
return num > 0
}
// 是否可以被 3 整除(为 true 的值放在后面)
func canBeDividedBy3(num int) bool {
return num % 3 == 0
}
性能对比
从扩展性上看,显然第二种解法比第一种好很多,除此之外,我们在第二种解法中还通过指针移动和位运算的方式优化了程序的性能,具体对性能的影响如何,可以编写基准测试来验证:
package main
import (
"testing"
)
func BenchmarkReOrderArrayV1(b *testing.B) {
for n := 0; n < b.N; n++ {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
reOrderArrayV1(arr) // run reOrderArrayV1(arr) b.N times
}
}
func BenchmarkReOrderArrayV2(b *testing.B) {
for n := 0; n < b.N; n++ {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
reOrderArrayV2(arr, isEven) // run reOrderArrayV2(arr, isEven) b.N times
}
}
运行上面的基准测试代码:
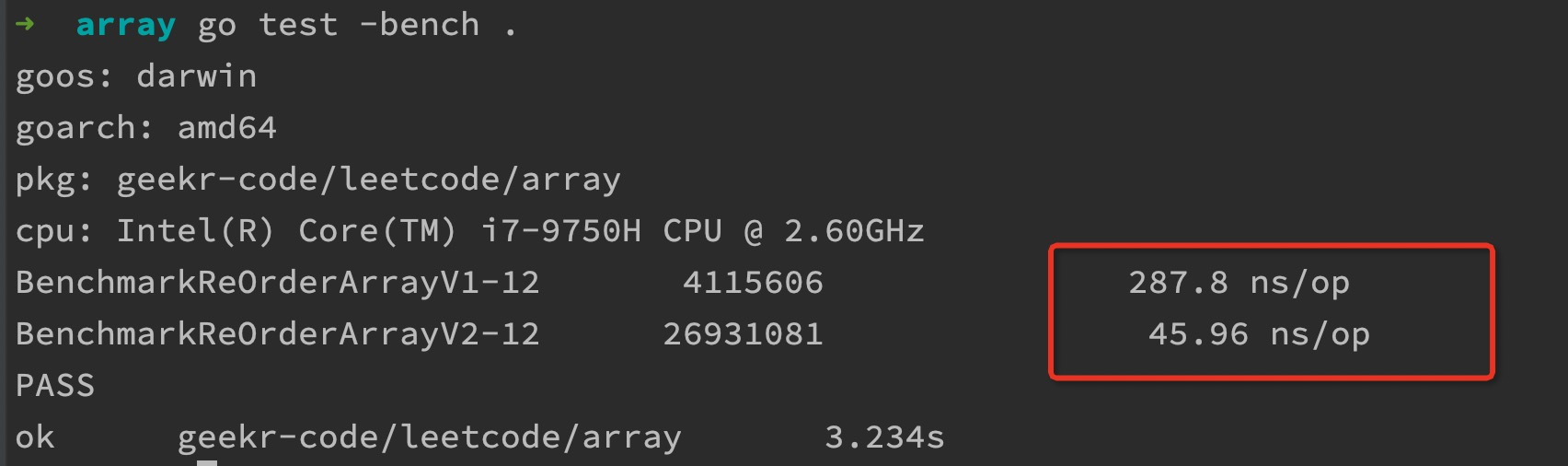
可以看到 reOrderArrayV2 排序函数的单次运行时间要比 reOrderArrayV1 快 6 倍,性能有了很显著的提升。
此外,还可以加上 -benchmem 选项对比下两种解法的内存分配情况(空间复杂度),由于第一种解法需要引入额外的数组切片存储中间数据,所以显然第二种解法的空间复杂度更优:
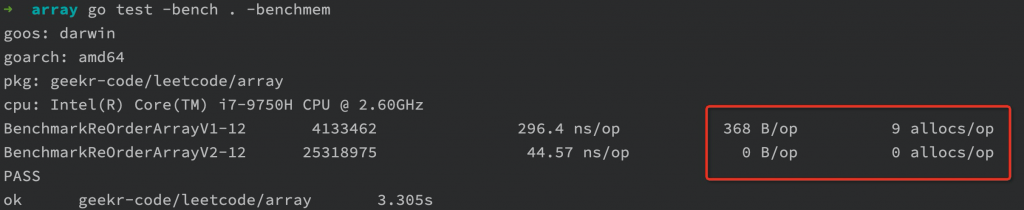
可以看到,第一种解法每次要分配 368B 的内存空间,而第二种解法不需要额外分配内存空间。
通过上面的对比,你觉得自己是初级程序员还是资深程序员呢?或者你还有没有更优的解法呢?欢迎通过下面的评论框展示你的能力。