实现原理
今天介绍比前面三种排序算法性能更好的排序算法 —— 归并排序。
所谓归并排序,指的是如果要排序一个数据序列,我们可以先把该序列从中间分成前后两部分,然后对这两部分分别做排序操作,再将排好序的两部分合并在一起,这样整个数据序列就都有序了。
归并排序使用了分治思想,分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。说到这里,可能你会联想起我们之前讲到的一个编程技巧 —— 递归,没错,归并排序就是通过递归来实现的。这个递归的公式是每次都将传入的待排序数据序列一分为二,直到变成不能继续分割的最小区间单元,然后将最小区间单元数据排序后合并起来,最终返回的就是排序好的数据序列了。图示如下:
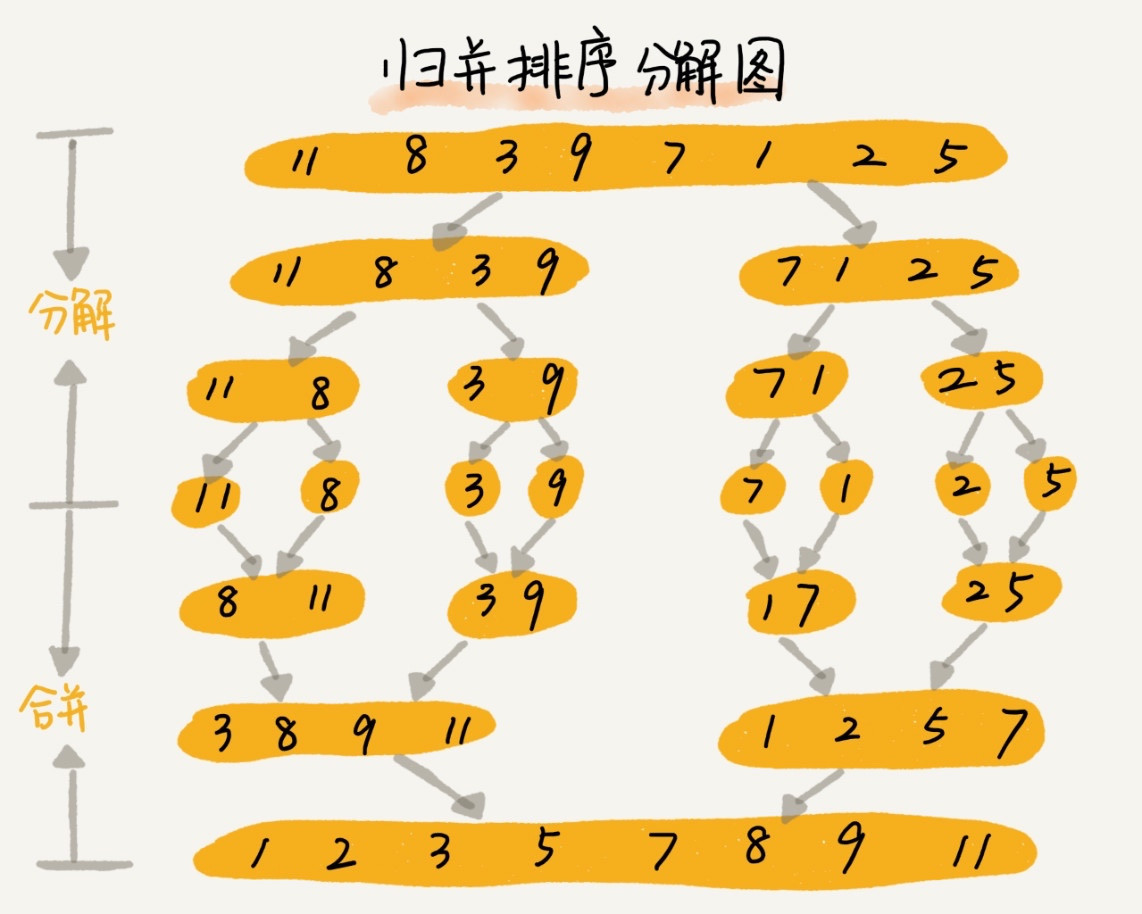
由于涉及到递归,所以归并排序从理解上要比前面三个排序要困难一些,还是建议通过这个动态图帮助理解:https://visualgo.net/zh/sorting(在界面顶部选择归并排序,然后在左下角点击执行即可)。
示例代码
通过上面的分析,我们知道归并=递归+合并,对应的 Go 实现代码如下:
package main
import (
"fmt"
)
// 归并排序
func mergeSort(nums []int) []int {
if len(nums) <= 1 {
return nums
}
// 获取分区位置
p := len(nums) / 2
// 通过递归分区
left := mergeSort(nums[0:p])
right := mergeSort(nums[p:])
// 排序后合并
return merge(left, right)
}
// 排序合并
func merge(left []int, right []int) []int {
i, j := 0, 0
m, n := len(left), len(right)
// 用于存放结果集
var result []int
for {
// 任何一个区间遍历完,则退出
if i >= m || j >= n {
break
}
// 对所有区间数据进行排序
if left[i] <= right[j] {
result = append(result, left[i])
i++
} else {
result = append(result, right[j])
j++
}
}
// 如果左侧区间还没有遍历完,将剩余数据放到结果集
if i != m {
for ; i < m; i++ {
result = append(result, left[i])
}
}
// 如果右侧区间还没有遍历完,将剩余数据放到结果集
if j != n {
for ; j < n; j++ {
result = append(result, right[j])
}
}
// 返回排序后的结果集
return result
}
func main() {
nums := []int{4, 5, 6, 7, 8, 3, 2, 1}
sortedNums := mergeSort(nums)
fmt.Println(sortedNums)
}
运行上述代码,打印结果如下:

性能分析
最后我们来看下归并排序的性能:
- 归并排序不涉及相等元素位置交换,是稳定的排序算法;
- 时间复杂度是 O(nlogn),要优于冒泡排序和插入排序的 O(n2);
- 归并排序需要额外的空间存放排序数据,不是原地排序,最多需要和待排序数据序列同样大小的空间,所以空间复杂度是 O(n)。
归并排序的时间复杂度推导过程
归并的思路时将一个复杂的问题 a 递归拆解为子问题 b 和 c,再将子问题计算结果合并,最终得到问题的答案,这里我们将归并排序总的时间复杂度设为 T(n),则 T(n) = 2*T(n/2) + n,其中 T(n/2) 是递归拆解的第一步对应子问题的时间复杂度,n 则是排序合并函数的时间复杂度(一个循环遍历),依次类推,我们可以推导 T(n) 的计算逻辑如下:
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= ...
= 2^k*T(n/2^k) + k*n
递归到最后,T(n/2k)≈T(1),也就是 n/2k = 1,计算归并排序的时间复杂度,就演变成了计算 k 的值,2k = n,所以 k=log2n,我们把 k 的值带入上述 T(n) 的推导公式,得到:
T(n) = n*T(1) + n*log2n = n(C + log2n)
注:上述公式中 2 是下标,即 log2n。
把常量和低阶忽略,所以 T(n) = nlogn。